题目内容
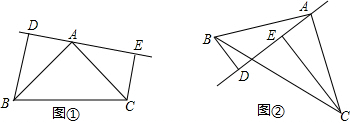
1. 已知:如图,在△ABC中,BD,CE分别是边AC,AB上的高,点F在BC上,BF=CF,则图中与EF相等的线段是BF、CF、DF.
已知:如图,在△ABC中,BD,CE分别是边AC,AB上的高,点F在BC上,BF=CF,则图中与EF相等的线段是BF、CF、DF.
分析 根据BD,CE分别是边AC,AB上的高,可得∠BEC=∠CDB=90°,再根据BF=CF可得F为BC中点,再根据直角三角形斜边上的中线等于斜边的一半可得EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,进而可得答案.
解答 解:∵BD,CE分别是边AC,AB上的高,
∴∠BEC=∠CDB=90°,
∵BF=CF,
∴F为中点,
∴EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,
∴EF=DF,
∴EF=DF=BF=FC,
故答案为:BF、CF、DF.
点评 此题主要考查了直角三角形的性质,关键是掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
3.已知实数x,y满足$\sqrt{x-1}$+|y+3|=0,则3x+2y的值为( )
| A. | -2 | B. | 3 | C. | $\frac{25}{8}$ | D. | -4 |
13.不解方程,判别一元二次方程2x2-6x=1的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 无法确定 |
 如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,拱高CD=7米,求圆的半径.
如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,拱高CD=7米,求圆的半径.
 如图,一轴对称图形画出它的一半,请你以图中虚线为对称轴画出它的另一半.
如图,一轴对称图形画出它的一半,请你以图中虚线为对称轴画出它的另一半. 已知数轴上点A,B,C所表示的数分别是4,-5,x.
已知数轴上点A,B,C所表示的数分别是4,-5,x.