Question

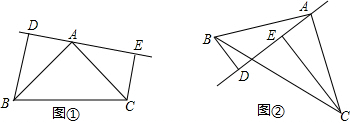
12．已知：如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于点D，CE⊥DE于点E，且AD=CE．
（1）若BC在DE的同侧（如图①）求证：BA⊥AC．
（2）若BC在DE的两侧（如图②），问AB与AC仍垂直吗？若是请予证明，若不是请说明理由．

Answer 1

分析 （1）根据直角三角形全等的判定方法HL易证得△ABD≌△CAE，可得∠DAB=∠ACE，再根据三角形内角和定理即可证得结论；
（2）与（1）同理结论仍成立．

解答 证明：∵BD⊥DE于D，CE⊥DE于E，
∴∠ADB=∠CEA=90°，
在Rt△ADB和Rt△CEA中，
$\left\{\begin{array}{l}{AB=CA（已知）}\\{AD=CE（已知）}\end{array}\right.$
∴Rt△ABD≌Rt△CAE（HL），
∴∠DAB=∠ACE．
又∵∠ACE+∠CAE=90°，
∴∠DAB+∠CAE=90°
∴∠BAC=90°，
即AB⊥AC；
（2）AB⊥AC
∵BD⊥DE于D，CE⊥DE于E，
∴∠ADB=∠CEA=90°，
在Rt△ADB和Rt△CEA中，
$\left\{\begin{array}{l}{AB=CA（已知）}\\{AD=CE（已知）}\end{array}\right.$
∴Rt△ABD≌Rt△CAE（HL），
∴∠DAB=∠ACE．
又∵∠ACE+∠CAE=90°，
∴∠DAB+∠CAE=90°
∴∠BAC=90°，
即AB⊥AC．

点评 本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解题的关键，属中档题．