题目内容
已知实数a,b是直角△ABC的两条直角边,且满足(a2+b2+25)(a2+b2-25)=0,a+b=2+
,求△ABC的面积.
| 21 |
考点:一元二次方程的应用
专题:
分析:再将根据(a2+b2+25)(a2+b2-25)=0,可得a2+b2-25=0,将方程变形为(a+b)2-2ab-25=0,再将a+b=2+
代入,求出ab的结果,进一步即可求解.
| 21 |
解答:解:∵(a2+b2+25)(a2+b2-25)=0,
∴a2+b2-25=0,
(a+b)2-2ab-25=0,
将a+b=2+
代入,可得(2+
)2-2ab-25=0
解得ab=2
,
ab=
.
故△ABC的面积是
.
∴a2+b2-25=0,
(a+b)2-2ab-25=0,
将a+b=2+
| 21 |
| 21 |
解得ab=2
| 21 |
| 1 |
| 2 |
| 21 |
故△ABC的面积是
| 21 |
点评:本题考查了一元二次方程的应用,解题的关键将式子变形得到(a+b)2-2ab-25=0,求得ab的结果.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
下列说法错误的是( )
| A、一个三角形中至少有一个角不少于60° |
| B、三角形的中线不可能在三角形的外部 |
| C、三角形的中线把三角形的面积平均分成相等的两部分 |
| D、直角三角形只有一条高 |
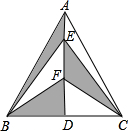 如图,在△ABC中,AD是BC边上的高,点E、F是AD上的两点,AB=AC,BC=4,AD=3,则图中阴影部分的面积是( )
如图,在△ABC中,AD是BC边上的高,点E、F是AD上的两点,AB=AC,BC=4,AD=3,则图中阴影部分的面积是( ) 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按