题目内容
某市出租车的计价规定如下:当行驶路程小于3千米时,乘车费用都是5元(即起步价5元),再加2元燃油费;当行驶路程大于或等于3千米时,超过3千米的部分按每0.5千米收费0.9元,再加2元燃油费.
(1)请写出乘车费用y(元)与行驶路程x(千米)之间的函数关系;
(2)按常规,乘车付费时按计费器上显示的金额进行“四舍五入”后取整,小赵一次乘车后付费12元,请你确定小赵这次乘车路程x的取值范围.
(1)请写出乘车费用y(元)与行驶路程x(千米)之间的函数关系;
(2)按常规,乘车付费时按计费器上显示的金额进行“四舍五入”后取整,小赵一次乘车后付费12元,请你确定小赵这次乘车路程x的取值范围.
考点:一次函数的应用
专题:
分析:(1)根据车费=起步价+超过3千米的路程×2×0.9+4列式即可;
(2)把y=12代入(1)得到的代数式求得x值,进一步确定范围即可.
(2)把y=12代入(1)得到的代数式求得x值,进一步确定范围即可.
解答:解:(1)∵当行驶路程小于3千米时,乘车费用都是5元(即起步价5元),再加2元燃油费;当行驶路程大于或等于3千米时,超过3千米的部分按每0.5千米收费0.9元,再加2元燃油费;
∴当x≤3时,y=7;
当x>3时,y=7+(x-3)÷0.5×0.9+2=1.8x+3.6;
(2)∵小赵一次乘车后付费12元,
∴依题意得:1.8x+3.6=12
解得x≈4.7.
所以小赵这次乘车路程4.5≤x<5.
∴当x≤3时,y=7;
当x>3时,y=7+(x-3)÷0.5×0.9+2=1.8x+3.6;
(2)∵小赵一次乘车后付费12元,
∴依题意得:1.8x+3.6=12
解得x≈4.7.
所以小赵这次乘车路程4.5≤x<5.
点评:此题考查了一次函数的应用,对于不同范围内的出租车付费问题;得到超过3千米的车费的代数式是解决本题的关键.

练习册系列答案
相关题目
 如图,BI、CI分别平分∠ABD和∠ACD,∠A=40°,∠D=160°,则∠I是( )
如图,BI、CI分别平分∠ABD和∠ACD,∠A=40°,∠D=160°,则∠I是( )| A、60° | B、80° |
| C、90° | D、100° |
下列函数:xy=1,y=
,y=
,y=
,y=2x2中,是y关于x的反比例函数的有( )个.
| x |
| 3 |
| k |
| y |
| 1 |
| x-2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
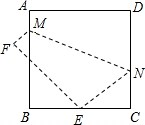 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN. 如图,∠1=∠2,
如图,∠1=∠2,