题目内容
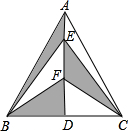 如图,在△ABC中,AD是BC边上的高,点E、F是AD上的两点,AB=AC,BC=4,AD=3,则图中阴影部分的面积是( )
如图,在△ABC中,AD是BC边上的高,点E、F是AD上的两点,AB=AC,BC=4,AD=3,则图中阴影部分的面积是( )| A、12 | B、6 | C、3 | D、4 |
考点:轴对称的性质
专题:
分析:根据等腰三角形性质求出BD=DC,AD⊥BC,推出△CEF和△BEF关于直线AD对称,得出S△BEF=S△CEF,根据图中阴影部分的面积是
S△ABC求出即可.
| 1 |
| 2 |
解答:解:∵AB=AC,BC=4,AD是△ABC的中线,
∴BD=DC=
BC=2,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:
×BC×AD=
×3×4=6,
∴图中阴影部分的面积是
S△ABC=3.
故选C.
∴BD=DC=
| 1 |
| 2 |
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
∴图中阴影部分的面积是
| 1 |
| 2 |
故选C.
点评:本题考查了勾股定理、轴对称的性质.通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 如图,点A、B在圆O上,△OAB是等边三角形,延长OA到C,使得AC=OA,连接BC.在圆O上是否存在一点D,使得BD=BC?
如图,点A、B在圆O上,△OAB是等边三角形,延长OA到C,使得AC=OA,连接BC.在圆O上是否存在一点D,使得BD=BC?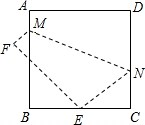 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.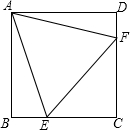 如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上.
如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上.