题目内容
已知抛物线y=x2+(m+1)x-m-2(m<3)的图象与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴在y轴的左侧,求△ABC的面积S的取值范围.
考点:抛物线与x轴的交点
专题:
分析:首先求出A,B两点的坐标以及C的坐标,进而可表示出△ABC的面积S,再根据抛物线的对称轴在y轴的左侧,可求出m的取值范围,又因为m<3,所以△ABC的面积S的取值范围可求出.
解答:解:∵y=x2+(m+1)x-m-2=(x-1)(x+m+2),
∴0=(x-1)(x+m+2)得解是
x=-1或x=-m-2,
∴AB=|-m-2+1|=|-m-1|,
设x=0,则y=-m-2,
∴OC=|-m-2|,
∴△ABC的面积S=
|-m-1|•|-m-2|,
∵抛物线的对称轴在y轴的左侧,
∴-
<0,
∴-
<0,
∴m>-1,
∵m<3,
∴-1<m<3,
∴S的最大值是10,S的最小值是0.5,
∴0.5<S<10.
∴0=(x-1)(x+m+2)得解是
x=-1或x=-m-2,
∴AB=|-m-2+1|=|-m-1|,
设x=0,则y=-m-2,
∴OC=|-m-2|,
∴△ABC的面积S=
| 1 |
| 2 |
∵抛物线的对称轴在y轴的左侧,
∴-
| b |
| 2a |
∴-
| m+1 |
| 2 |
∴m>-1,
∵m<3,
∴-1<m<3,
∴S的最大值是10,S的最小值是0.5,
∴0.5<S<10.
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物和坐标轴的交点、三角形面积的求法等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
下列函数:xy=1,y=
,y=
,y=
,y=2x2中,是y关于x的反比例函数的有( )个.
| x |
| 3 |
| k |
| y |
| 1 |
| x-2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
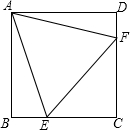 如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上.
如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上. 有理数a、b在数轴上对应点如图所示:
有理数a、b在数轴上对应点如图所示: