题目内容
1.用火柴棍象如图这样搭三角形:你能找出规律猜想出下列问题吗?搭n个三角形需要( )根火柴棍.
| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 3n. |
分析 易得第1个图形中火柴的根数为3,得到其余图形中火柴的根数在3的基础上增加几个2即可.
解答 解:搭1个三角形需要2×1+1=3根火柴棍;
搭2个三角形需要2×2+1=5根火柴棍;
搭3个三角形需要2×3+1=7根火柴棍;
搭4个三角形需要2×4+1=9根火柴棍;
…
依此类推,可以发现,搭几个三角形需要火柴棍的根数就是2与几的乘积加1.
所以,搭n个三角形需要2×n+1=2n+1根火柴棍.
故选B.
点评 本题考查了图形的变化类题目,主要考查了学生通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
相关题目
11.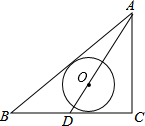 如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
 如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )| A. | 1 | B. | $\frac{6}{7}$ | C. | $\frac{2}{3}$ | D. | 1.5 |
9.已知点A(m,n)(n≠0)在平面直角坐标系中,则下列各点中,与点关于x轴对称的是( )
| A. | (-m,n) | B. | (m,-n) | C. | (-m,-n) | D. | (n,m) |
16.如图的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.计算(-18)÷(-3)的结果为( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
10.下列说法正确的有( )
| A. | 立方根是它本身的数是0和1 | B. | 异号两数相加,结果为负数 | ||
| C. | 非负数绝对值是它本身 | D. | 没有平方根的数也没有立方根 |
 如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为7.5.
如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为7.5.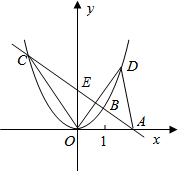 如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B、C两点,点B的坐标为(1,1).
如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B、C两点,点B的坐标为(1,1).