题目内容
11. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$+2 |
分析 根据角平分线的性质即可求得CD的长,然后在直角△BDE中,根据30°的锐角所对的直角边等于斜边的一半,即可求得BD长,则BC即可求得.
解答 解:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故选C.
点评 本题考查了角的平分线的性质以及直角三角形的性质,30°的锐角所对的直角边等于斜边的一半,理解性质定理是关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
6. 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )| A. | $\frac{1}{{2}^{2015}}$ | B. | $\frac{1}{{2}^{2014}}$ | C. | 1-$\frac{1}{{2}^{2015}}$ | D. | 2-$\frac{1}{{2}^{2014}}$ |
20.学校机房今年和去年共购置了100台计算机,已知今年购置计算机数量是去年购置计算机数量的3倍,则今年购置计算机的数量是( )
| A. | 25台 | B. | 50台 | C. | 75台 | D. | 100台 |
 已知,∠ABC=∠DBE=90°,且AB=BC,BE=BD,说明:S△ABE=S△BCD.
已知,∠ABC=∠DBE=90°,且AB=BC,BE=BD,说明:S△ABE=S△BCD.

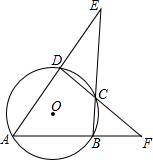 如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,