题目内容
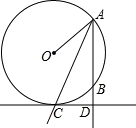
如图，已知OA是圆O的半径，点B在圆O上，∠OAB的平分线AC交圆O于点C，CD⊥AB于点D，求证：CD是圆O的切线．
【考点】切线的判定．
【专题】证明题．
【分析】连结OC，根据角平分线的定义和等腰三角形的性质得出∠OCA=∠DAC，证出OC∥AD，由CD⊥AD，得出CD⊥OC，然后根据切线的判定定理即可得到结论．
【解答】证明：连结OC，如图，
∵AC为∠OAB的平分线，
∴∠OAC=∠DAC，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠OCA=∠DAC，
∴OC∥AD，
∵CD⊥AD，
∴CD⊥OC，
∴CD是圆O的切线．
【点评】本题考查了切线的判定定理、等腰三角形的性质、平行线的判定与性质；熟练掌握切线的判定方法，证出OC∥AD是解决问题的关键．
练习册系列答案
小学课时特训系列答案
相关题目
______．
C．
D．
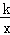的图象与一次函数y2=ax+b的图象交于点A（1，4）和点（m，﹣2），则满足y1＞y2的自变量x的取值范围是__________．
=
