题目内容
已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,﹣3)
(1)求此二次函数的解析式以及顶点D的坐标;
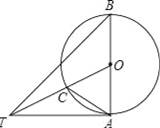
(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.
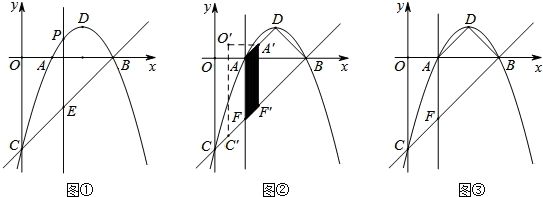
(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA、DB、四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.
【考点】二次函数综合题.
【分析】(1)利用待定系数法即可求得抛物线的解析式,然后化为顶点式即可求得顶点的坐标.
(2)先求得直线BC的解析式,设P(x,﹣x2+4x﹣3),则F(x,x﹣3),根据PF等于P点的纵坐标减去F点的纵坐标即可求得PF关于x的函数关系式,从而求得P的坐标和PF的最大值;
(3)线利用待定系数法求得直线AD的解析式为y=x﹣1,直线BC的解析式为:y=x﹣3,从而得到AD∥BC,且与x轴正半轴夹角均为45°,由平行于与y轴的直线上点的坐标特点可求得F(1,﹣2),从而可求得AF=2,由当点C与点F重合时立即停止运动,可知0≤t≤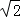 ,由AF∥A′F′,AD∥C′B,可知四边形AFF′A′为平行四边形,根据由平行四边形的面积公式可知当t=
,由AF∥A′F′,AD∥C′B,可知四边形AFF′A′为平行四边形,根据由平行四边形的面积公式可知当t=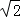 时,重合部分的面积最大,设A′F′与x轴交于点K,依据特殊锐角三角函数值可求得AK=1.依据平行四边形的面积公式可求得重合部分的最大面积为2.
时,重合部分的面积最大,设A′F′与x轴交于点K,依据特殊锐角三角函数值可求得AK=1.依据平行四边形的面积公式可求得重合部分的最大面积为2.
【解答】解:(1)设抛物线的解析式为y=a(x﹣1)(x﹣3),将点C的坐标代入得:3a=﹣3,
解得:a=﹣1.
∵将a=﹣1代入得:y=﹣(x﹣1)(x﹣3)=﹣x2+4x﹣3.
∴抛物线的解析式为y=﹣x2+4x﹣3.
由抛物线的对称轴方程可知:x=﹣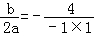 =2,
=2,
将x=2代入抛物线的解析式得:y=1.
∴点D的坐标为(2,1).
(2)存在.
理由:设直线BE的解析式为y=kx+b.
将B(3,0),C(0,﹣3)代入上式,得: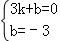 ,
,
解得:k=1,b=﹣3.
则直线BC的解析式为y=x﹣3.
∵PE∥y轴,
∴点P与点E的横坐标均为m.
∵将x=m代入直线BC的解析式的y=m﹣3,
∴点E的坐标为(m﹣3).
将x=m代入抛物线的解析式得y=﹣m2+4m﹣3,
∴点P的坐标为(m,﹣m2+4m﹣3).
∴PE═﹣m2+4m﹣3﹣(m﹣3)=﹣m2+3m=﹣(m2﹣3m+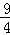 ﹣
﹣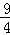 )=﹣(m﹣
)=﹣(m﹣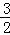 )2+
)2+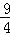 .
.
∴当m=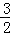 时,PE的长有最大值,最大值为
时,PE的长有最大值,最大值为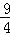 .
.
(3)如图所示:
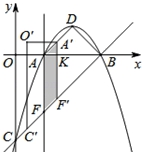
∵A(1,0)、B(3,0)、D(2,1)、C(0,﹣3),
∴可求得直线AD的解析式为:y=x﹣1;直线BC的解析式为:y=x﹣3.
∴AD∥BC,且与x轴正半轴夹角均为45°.
∵AF∥y轴,
∴F(1,﹣2),
∴AF=2.
∵当点C与点F重合时立即停止运动,
∴0≤t≤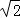 .
.
∵AF∥A′F′,AD∥C′B,
∴四边形AFF′A′为平行四边形.
∵当AA′有最大值时,重合部分的面积最大.
∴当t=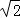 时,重合部分的面积最大.
时,重合部分的面积最大.
设A′F′与x轴交于点K,则AK=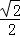 AA′=
AA′=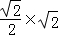 =1.
=1.
∴S=S▱AFF′A′=AF•AK=2×1=2.
四边形OAFC与四边形ADBF重叠部分面积S的最大值为2.
【点评】本题是二次函数综合题,考查了二次函数的图象与性质、待定系数法求解析式、最值、平行四边形、等腰直角三角形、图形面积计算等知识点.列出线段PE的表达式是解决问题(2)的关键,证得四边形AFF′A′为平行四边形是解答问题(3)关键.

 BC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC等于( ).
BC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC等于( ).

 (D)
(D)
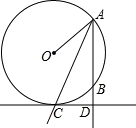

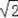
 B.2 C.
B.2 C.