题目内容
如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.
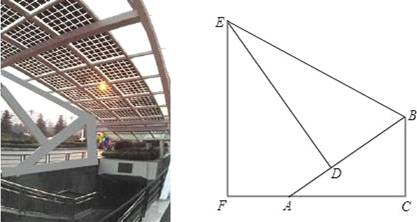

【考点】解直角三角形的应用.
【分析】过B作BH⊥EF于点H,在Rt△ABC中,根据∠BAC=30°,BC=1.5,可求得AB的长度,又AD=1m,可求得BD的长度,在Rt△EBD中解直角三角形求得EB的长度,然后根据BH⊥EF,求得∠EBH=30°,继而可求得EH的长度,易得EF=EH+HF的值.
【解答】解:过B作BH⊥EF于点H,
∴四边形BCFH为矩形,BC=HF=1.5m,∠HBA=∠BAC=30°,
在Rt△ABC中,
∵∠BAC=30°,BC=1.5m,
∴AB=3m,
∵AD=1m,
∴BD=2m,
在Rt△EDB中,
∵∠EBD=60°,
∴∠BED=90°﹣60°=30°,
∴EB=2BD=2×2=4m,
又∵∠HBA=∠BAC=30°,
∴∠EBH=∠EBD﹣∠HBD=30°,
∴EH=
 EB=2m,
EB=2m,
∴EF=EH+HF=2+1.5=3.5(m).
答:该支架的边BE为4m,顶端E到地面的距离EF的长度为3.5m.


【点评】本题考查了解直角三角形的应用,解题的关键是将实际问题转化为数学问题,构造直角三角形并解直角三角形,难度适中.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
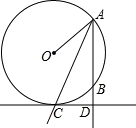


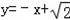
 的距离等于2的点共有( )
的距离等于2的点共有( )