题目内容
12.(1)计算:$\root{3}{-8}$-$\sqrt{(-1)^{2}}$+$\sqrt{36}$(2)解方程组:$\left\{\begin{array}{l}{x+2y=1}\\{3x-2y=11}\end{array}\right.$
(3)解不等式组:$\left\{\begin{array}{l}{x-2>0}\\{2(x+1)≥3x-1}\end{array}\right.$.(将不等式组解集在数轴上表示出来)
分析 (1)原式利用立方根,以及平方根定义计算即可得到结果;
(2)方程组利用加减消元法求出解即可;
(3)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=-2-1+6=-3;
(2)$\left\{\begin{array}{l}{x+2y=1①}\\{3x-2y=11②}\end{array}\right.$,
①+②得:4x=12,即x=3,
将x=3代入①,得:y=-1
∴原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{x-2>0①}\\{2(x+1)≥3x-1②}\end{array}\right.$,
由①得:x>2,
由②得:x≤3,
将不等式组的解集在数轴上表示出来: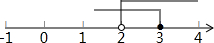
∴原不等式组的解集为2<x≤3.
点评 此题考查了实数的运算,解二元一次方程组,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | x2•x3=x6 | B. | x5+x5=2x10 | C. | (-2x)3=8x3 | D. | (-2x3)÷(-6x2)=$\frac{1}{3}$x |
7.在平面直角坐标系中,点P(1,-2)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.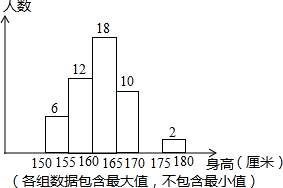 如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
 如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )
如图是初一某班全体50位同学身高情况的频数分布直方图,则身高在160-165厘米的人数的频率是( )| A. | 0.36 | B. | 0.46 | C. | 0.56 | D. | 0.6 |