题目内容
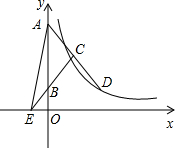 如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=
如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=| k |
| x |
考点:反比例函数系数k的几何意义,等腰三角形的性质
专题:
分析:作CF⊥y轴于F,连结BD.先由等腰三角形三线合一的性质得出AF=FB,而CD=AC,那么CF是△ABD的中位线,于是CF∥BD.再设B(0,b),则D(
,b),设AB=c,则F(0,b+
c),A(0,b+c),C(
,b+
c),由△ABE的面积为5,得出
c•OE=5①,由CF∥OE,得出
c•OE=b•
=
②,比较①②,得
=5,即可求出k=10.
| k |
| b |
| 1 |
| 2 |
| k |
| 2b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2b |
| k |
| 2 |
| k |
| 2 |
解答: 解:如图,作CF⊥y轴于F,连结BD.
解:如图,作CF⊥y轴于F,连结BD.
∵CA=CB,CF⊥y轴于F,
∴AF=FB,
∵CD=AC,
∴CF是△ABD的中位线,
∴CF∥BD,CF=
BD.
设B(0,b),则D(
,b),
设AB=c,则F(0,b+
c),A(0,b+c),C(
,b+
c),
∵△ABE的面积为5,
∴
AB•OE=5,即
c•OE=5①.
∵CF∥OE,
∴
=
,即
=
,
∴
c•OE=b•
=
②,
比较①②,得
=5,
∴k=10.
故答案为10.
 解:如图,作CF⊥y轴于F,连结BD.
解:如图,作CF⊥y轴于F,连结BD.∵CA=CB,CF⊥y轴于F,
∴AF=FB,
∵CD=AC,
∴CF是△ABD的中位线,
∴CF∥BD,CF=
| 1 |
| 2 |
设B(0,b),则D(
| k |
| b |
设AB=c,则F(0,b+
| 1 |
| 2 |
| k |
| 2b |
| 1 |
| 2 |
∵△ABE的面积为5,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∵CF∥OE,
∴
| CF |
| OE |
| BF |
| OB |
| ||
| OE |
| ||
| b |
∴
| 1 |
| 2 |
| k |
| 2b |
| k |
| 2 |
比较①②,得
| k |
| 2 |
∴k=10.
故答案为10.
点评:本题考查了等腰三角形的性质,反比例函数图象上点的坐标特征,三角形的面积,平行线分线段成比例定理,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
下列命题是真命题的是( )
| A、平分弦的直径垂直于弦 |
| B、一组数据1,5,3,4,5,6的中位数为5 |
| C、等腰三角形是中心对称图形 |
| D、三角形的外心是它三边垂直平分线的交点 |
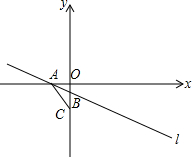 如图,已知直线l:y=-
如图,已知直线l:y=-
 如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,求∠A.
如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,求∠A.