题目内容
 如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,求∠A.
如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,求∠A.考点:三角形内角和定理
专题:
分析:在△BOC中可求得∠OBC+∠OCB,再由角平分线的性质可求得∠ABC+∠ACB,再利用三角形内角和定理可求出∠A.
解答:解:
∵∠BOC=110°,
∴∠OBC+∠OCB=180°-∠BOC=180°-110°=70°,
∴2(∠OBC+∠OCB)=140°,
即∠ABC+∠ACB=140°,
∴∠A=180°-(∠ABC+∠ACB)=180°-140°=40°.
∵∠BOC=110°,
∴∠OBC+∠OCB=180°-∠BOC=180°-110°=70°,
∴2(∠OBC+∠OCB)=140°,
即∠ABC+∠ACB=140°,
∴∠A=180°-(∠ABC+∠ACB)=180°-140°=40°.
点评:本题主要考查三角形内角和定理,由条件求得∠ABC+∠ACB=140°是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
有甲、乙两块铁板(厚度忽略不计),甲的形状为直角梯形,两底边长分别为4cm,10cm,且有一内角为60°;乙的形状为等腰三角形,其顶角为45°,腰长12cm.在不改变形状的前提下,试图分别把它们从一个直径为8.7cm的圆洞中穿过,结果是( )
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
某校共1380人参加中考,为了考查这1380名学生的外语成绩,从中抽取了80名学生的外语成绩进行调查,以下说法正确的是( )
| A、某校1380名学生的成绩是总体 |
| B、样本容量是80人 |
| C、其中80名学生的外语成绩是总体的一个样本 |
| D、每个学生是个体 |
函数y=ax+a与y=
(a≠0)在同一直角坐标系中的图象可能是( )
| a |
| x |
A、 |
B、 |
C、 |
D、 |
 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,
如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,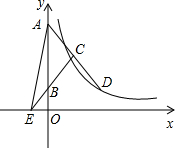 如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=
如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y= 如图,一束光线与水平镜面的夹角为α,该光线先照射到平面镜上,然后在两个平面镜上反射.如果∠α=60°,∠β=50°,那么∠γ=
如图,一束光线与水平镜面的夹角为α,该光线先照射到平面镜上,然后在两个平面镜上反射.如果∠α=60°,∠β=50°,那么∠γ=