题目内容
13.在下列数列里,写出后面三个数及第n个数(1)1,4,9,16,25,36,49…n2;
(2)1,11,21,31,41,51,61,71…10n-9;
(3)2,4,8,16,32,64,128,256…2n;
(4)$\frac{1}{3}$,$\frac{5}{6}$,$\frac{9}{9}$,$\frac{13}{12}$,$\frac{17}{15}$,$\frac{21}{18}$,$\frac{25}{21}$,$\frac{29}{24}$…$\frac{4n-3}{3n}$;
(5)$\frac{1}{2}$,$\frac{2}{5}$,$\frac{3}{10}$,$\frac{4}{17}$,$\frac{5}{26}$,$\frac{6}{37}$,$\frac{7}{50}$…$\frac{n}{{n}^{2}+1}$;
(6)0,3,8,15,24,35,48,63…n2-1.
分析 (1)这列数的每个数都等于它的项数的平方,据此解答即可.
(2)这列数构成以1为首项,以10为公差的等差数列,据此解答即可.
(3)这列数构成以2为首项,以2为公比的等比数列,据此解答即可.
(4)这列数的分子构成以1为首项,以4为公差的等差数列;这列数的分母构成以3为首项,以3为公差的等差数列,据此解答即可.
(5)这列数的分子分别是1、2、3、4、…,这列数的第n个数的分母是n2+1,据此解答即可.
(6)这列数中每个数与1的和都等于它的项数的平方,据此解答即可.
解答 解:根据分析,可得
(1)1,4,9,16,25,36,49,…,n2;
(2)1,11,21,31,41,51,61,71,…,10n-9;
(3)2,4,8,16,32,64,128,256,…,2n;
(4)$\frac{1}{3}$,$\frac{5}{6}$,$\frac{9}{9}$,$\frac{13}{12}$,$\frac{17}{15}$,$\frac{21}{18}$,$\frac{25}{21}$,$\frac{29}{24}$,…,$\frac{4n-3}{3n}$;
(5)$\frac{1}{2}$,$\frac{2}{5}$,$\frac{3}{10}$,$\frac{4}{17}$,$\frac{5}{26}$,$\frac{6}{37}$,$\frac{7}{50}$,…,$\frac{n}{{n}^{2}+1}$;
(6)0,3,8,15,24,35,48,63,…,n2-1.
故答案为:25,36,49,n2;51,61,71,10n-9;64,128,256,2n;$\frac{21}{18}$,$\frac{25}{21}$,$\frac{29}{24}$,$\frac{4n-3}{3n}$;$\frac{5}{26}$,$\frac{6}{37}$,$\frac{7}{50}$,$\frac{n}{{n}^{2}+1}$;35,48,63,n2-1.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律.

 口算题天天练系列答案
口算题天天练系列答案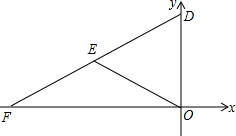 如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.
如图,平面直角坐标系中,O为坐标原点,已知直线y=$\frac{1}{2}$x+5分别与x,y轴相交于点F、D,点E在线段DF上,连接OE,且OE=DE.求OE所在的直线解析式.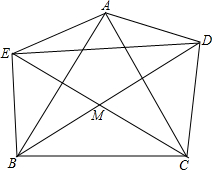 如图,△ABC中,D,E是△ABC外两点,M是△ABC内一点.若AE=BE,AD=DC,∠DEM=$\frac{1}{2}$∠AEB,∠EDM=$\frac{1}{2}$∠ADC.求证:MB=MC.
如图,△ABC中,D,E是△ABC外两点,M是△ABC内一点.若AE=BE,AD=DC,∠DEM=$\frac{1}{2}$∠AEB,∠EDM=$\frac{1}{2}$∠ADC.求证:MB=MC.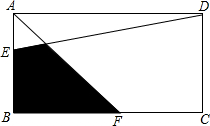 面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.
面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.