题目内容
4.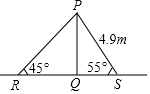 图中,PQ为一直立旗杆,PR及PS为两条已拉紧的绳,以将该旗杆固定在水平地面RQS上,PS的长度为4.9m,由R及S测得P的仰角分别为45°及55°.利用正弦公式,求R与S之间的距离.
图中,PQ为一直立旗杆,PR及PS为两条已拉紧的绳,以将该旗杆固定在水平地面RQS上,PS的长度为4.9m,由R及S测得P的仰角分别为45°及55°.利用正弦公式,求R与S之间的距离.
分析 先解直角△PQS,求出PQ与QS,再解直角△PQR,求出RQ,那么RS=RQ+QS.
解答 解:∵在直角△PQS中,∠PQS=90°,∠PSQ=55°,
∴sin∠PSQ=$\frac{PQ}{PS}$,∠SPQ=35°,
∴PQ=PS•sin∠PSQ=4.9×sin55°,
QS=PS•sin∠SPQ=4.9×sin35°,
∵在直角△PQR中,∠PQS=90°,∠PRQ=45°,
∴RQ=PQ=4.9×sin55°,
∴RS=RQ+QS=4.9×sin55°+4.9×sin35°=4.9(sin55°+sin35°).
故R与S之间的距离为4.9(sin55°+sin35°)m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,求出RQ与QS的值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.代数式$\sqrt{a+2}$在实数范围内有意义,实数a的取值范围是( )
| A. | a>2 | B. | a≥2 | C. | a>-2 | D. | a≥-2 |
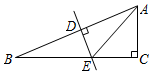 如图,Rt△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE=3$\sqrt{2}$.
如图,Rt△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE=3$\sqrt{2}$. 如图网格中每个小正方形的边长为1,阴影部分是一条可爱的小鱼,若把这条鱼剪拼成一个正方形,那么新正方形的边长是$\sqrt{6}$.
如图网格中每个小正方形的边长为1,阴影部分是一条可爱的小鱼,若把这条鱼剪拼成一个正方形,那么新正方形的边长是$\sqrt{6}$.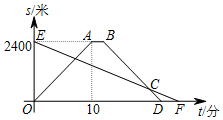 小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象. 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是40°.
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是40°.