题目内容
6.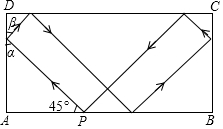 如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )
如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 20 | D. | 20$\sqrt{2}$ |
分析 根据勾股定理,可得斜边的长,根据线段的和差,可得答案.
解答 解:作GL⊥DC,如图 ,
,
设AE=x,ED=(4-x),
由勾股定理,得
PE=$\sqrt{2}$x,EF=$\sqrt{2}$(4-x),
同理GH=$\sqrt{2}$x,HI=$\sqrt{2}$(4-x),
PE+EF+GH+HI=$\sqrt{2}$(x+4-x+x+4-x)=8$\sqrt{2}$.
∵α=45°,∠FLG=90°,
∴FG=$\sqrt{2}$LG=4$\sqrt{2}$,
同理PI=4$\sqrt{2}$.
小球从P点被击出到回到点P,运动的总路程为
PE+EF+FG+GH+HI+IP=
=(PE+EF+GH+HI)+FG+IP
=8$\sqrt{2}$+4$\sqrt{2}$+4$\sqrt{2}$=16$\sqrt{2}$,
故选:B.
点评 本题考查了轨迹,利用勾股定理得出每段的长是解题关键.

练习册系列答案
相关题目
17.我们规定一个物体向右运动为正,向左运动为负.如果该物体向左连续运动两次,每次运动3 米,那么下列算式中,可以表示这两次运动结果的是( )
| A. | (-3)2 | B. | (-3)-(-3) | C. | 2×3 | D. | 2×(-3) |
14.已知△ABC的三边长分别为1、k、3,则化简|9-2k|-$\sqrt{4{k}^{2}-12k+9}$的结果是( )
| A. | 12-4k | B. | 6 | C. | -6 | D. | 4k-12 |
1.二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
根据表格,小明得出三个结论:①ac<0;②当x=2时,y=5;③x=3是方程ax2+(b-1)x+c=0的一个根,其中结论正确的共有( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
11.关于x的方程x2+2x+c=0有两个相等的实数根,则c的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
18.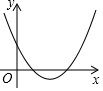 二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )
二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )
 二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )
二次函数y=2x2-2x+m(m为常数)的图象如图所示,如果当x=a时,y<0,那么当x=a-1时,函数值( )| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
16.下列每组数分别是三根木棒的长度,不能用它们摆成三角形的是( )
| A. | 5cm、8cm、12cm | B. | 6cm、8cm、12cm | C. | 5cm、6cm、8cm | D. | 5cm、6cm、12cm |
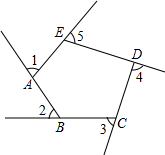 如图∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,∠1=∠2=∠3=∠4=70°,则∠AED=100°.
如图∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,∠1=∠2=∠3=∠4=70°,则∠AED=100°. 甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息,下列说法正确的个数为( )
甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息,下列说法正确的个数为( )