题目内容
14．已知△ABC的三边长分别为1、k、3，则化简|9-2k|-$\sqrt{4{k}^{2}-12k+9}$的结果是（ ）| A． | 12-4k | B． | 6 | C． | -6 | D． | 4k-12 |
分析 根据三边关系可知：2＜k＜4，从而可化简原式．
解答 解：由题意可知：2＜k＜4，
∴1＜9-2k＜5，1＜2k-3＜5，
∴原式=|9-2k|-$\sqrt{（2k-3）^{2}}$
=9-2k-2k+3
=12-4k
故选（A）
点评 本题考查二次根式的化简，解题的关键是根据题意得出k的范围，本题属于基础题型．
练习册系列答案
相关题目
小明和小颖在如图所示的四边形场地上，沿边骑自行车进行场地追逐赛（两人只要有一个人回到自己的出发点，则比赛结束）．小明从A地出发，沿A→B→C→D→A的路线匀速骑行，速度为8米/秒；小颖从B地出发，沿B→C→D→A→B的路线匀速骑行，速度为6米/秒．已知∠ABC=90°，AB=40米，BC=80米，CD=90米．设骑行时间为t秒，假定他们同时出发且每转一个弯需要额外耗时2秒．
2．在中考体育测试时，有六个男生引体向上的成绩分别是：11、10、13、17、10、23，对于这组数据，下列说法不正确的是（ ）
| A． | 平均数是14 | B． | 众数是10 | C． | 中位数是15 | D． | 方差是22 |
9．如果从-1，2，3三个数中任取一个数记作m，又从0，1，-2三个数中任取一个数记作n，那么点P（m，n）恰在第四象限的概率为（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{1}{9}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
19．王师傅每月都开着同一辆油电混合动力汽车从家出发到甲地果园进行志愿服务．纯燃油行驶时，耗油费用80元；纯电动行驶时，耗电费用30元．已知该汽车每行驶1千米，耗油费比耗电费多0.5元，求王师傅家到甲地果园的路程为多少千米？设王师傅家到甲地果园的路程为x千米，根据题意列出的方程是（ ）
| A． | 80+0.5x=30 | B． | 0.5x-80=30 | C． | $\frac{80}{x}$-0.5=$\frac{30}{x}$ | D． | $\frac{x}{80}$+0.5=$\frac{x}{30}$ |
6．
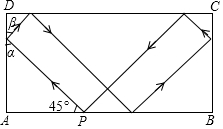如图，击打台球时小球反弹前后的运动路线遵循对称原理，即小球反弹前后的运动路线与台球案边缘的夹角相等（α=β），在一次击打台球时，把位于点P处的小球沿所示方向击出，小球经过5次反弹后正好回到点P，若台球案的边AD的长度为4，则小球从P点被击出到回到点P，运动的总路程为（ ）
如图，击打台球时小球反弹前后的运动路线遵循对称原理，即小球反弹前后的运动路线与台球案边缘的夹角相等（α=β），在一次击打台球时，把位于点P处的小球沿所示方向击出，小球经过5次反弹后正好回到点P，若台球案的边AD的长度为4，则小球从P点被击出到回到点P，运动的总路程为（ ）| A． | 16 | B． | 16$\sqrt{2}$ | C． | 20 | D． | 20$\sqrt{2}$ |
4．函数y=$\frac{1}{|x|+1}$的自变量x的取值范围是（ ）
| A． | x≠1 | B． | x≠-1 | C． | x≠0 | D． | 全体实数 |