题目内容
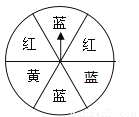
如图，转盘中6个小扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向红色区域的概率为 ．
．
【解析】
试题分析：∵圆被等分成6份，其中红色部分占2份，∴落在阴影区域的概率==，故答案为：．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
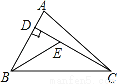
如图，已知在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于_____．
5
【解析】试题解析：
作EF⊥BC于F，
∵BE平分∠ABC，EF⊥BC，ED⊥AB，
∴EF=DE=2，
∴△BCE的面积
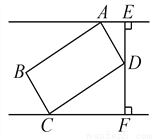
故答案为：5. 如图，矩形ABCD是供一机动车停放的车位示意图，已知BC＝2m，CD＝5.4m，∠DCF＝30°.请你计算车位所占的宽度EF约为多少米？(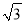
≈1.73，结果保留一位小数)
4.4米
【解析】试题分析：分别在Rt△BCF和Rt△AEF中求得DF和DE的长后，相加即可得到EF的长．
试题解析：
在Rt△DCF中，
∵CD=5.4m，∠DCF=30°，
∴sin∠DCF=，
∴DF=2.7m，
∵∠CDF+∠DCF=90°∠ADE+∠CDF=90°，
∴∠ADE=∠DCF=30°，
∵AD=BC=2，
∴cos∠... 下列说法中，正确的是（ ）
A. 不可能事件发生的概率为0
B. 随机事件发生的概率为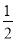
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币100次，正面朝上的次数一定为50次
A
【解析】试题分析：不可能事件发生的概率为0，故A正确；
随机事件发生的概率为在0到1之间，故B错误；
概率很小的事件也可能发生，故C错误；
投掷一枚质地均匀的硬币100次，正面向上的次数为50次是随机事件，D错误；
故选A． 如图所示，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6.
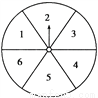
（1）若自由转动转盘，当它停止转动时，指针指向奇数区的概率是多少？
（2）请你用这个转盘设计一个游戏，当自由转动的转盘停止时，指针指向的区域的概率为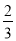
.
（1）；（2）详见解析．
【解析】试题分析：（1）自由转动转盘，当它停止转动时，指针指向数字的结果总共有6种，指针指向奇数区的结果有3种，所以指针指向奇数区的概率是．
（2）当自由转动的转盘停止时，指针指向的区域不大于4．（答案不唯一，符合要求即可）
试题解析：（1）指针指向奇数区的概率是．
（2）当自由转动的转盘停止时，指针指向的区域不大于4．（答案不唯一，符合要求即可）... 小球在如图所示的地板上自由滚动，并随机地停留在某块方砖上，每一块方砖除颜色外完全相同，它最终停留在黑色方砖上的概率是 ．
.
【解析】
试题分析：根据几何概率的求法：最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值．观察这个图可知：黑色区域（4块）的面积占总面积（9块）的，则它最终停留在黑色方砖上的概率是.
故答案为：． 某口袋中有20个球,每个球除颜色外都相同,其中白球x个,绿球2x个,其余为黑球,甲从袋中任意摸出一个球,若为绿球则获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.若对甲、乙双方公平,则x等于( )
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
根据题意得： ，即2x=20-x-2x，解得：x=4．故选B． 如图，在△ABC中，点P是△ABC三条角平分线的交点，则∠PBC＋∠PCA＋∠PAB=___度．
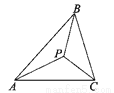
90
【解析】试题分析：由在△ABC中，点P是△ABC的内心，根据三角形的内心是三角形三条角平分线的交点，即可得∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，又由三角形内角和定理，即可求得∠PBC+∠PCA+∠PAB的度数．
试题解析：∵在△ABC中，点P是△ABC的内心，
∴∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，
∵∠ABC+∠BCA+... 如图是数轴的一部分,其单位长度为a,已知在△ABC中,AB=3a,BC=4a,AC=5a.用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法).
见解析
【解析】【试题分析】利用“SSS”作出三角形，作图方法见解析.
【试题解析】
如图.
作法如下:
(1)在数轴上截取AC=5a.
(2)分别以A,C为圆心,以3a,4a为半径画弧,两弧相交于点B.
(3)连接AB,BC,则△ABC即为所求作的三角形.