题目内容
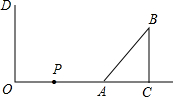 如图,在墙面OD(OD⊥OC)的右侧有一个Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,且OA=8cm,点P从点O出发,以1cm/s的速度在射线OA上运动,点Q在OD上运动,P、Q同时从O开始运动,设运动时间为t(s).
如图,在墙面OD(OD⊥OC)的右侧有一个Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,且OA=8cm,点P从点O出发,以1cm/s的速度在射线OA上运动,点Q在OD上运动,P、Q同时从O开始运动,设运动时间为t(s).(1)若△ABC与△POQ全等,则点Q的运动速度为
(2)当t为何值时,△ABP是直角三角形?
考点:全等三角形的判定,勾股定理的逆定理
专题:动点型
分析:(1)点Q的运动速度为xcm/s,则OQ=xtcm,OP=t•1=t(cm),由勾股定理求出AC=4cm,根据全等得出方程组,求出即可;
(2)根据题意得出两种情况,当∠BPA=90°时,此时P和C重合,当∠ABP=90°时,求出AP的长即可.
(2)根据题意得出两种情况,当∠BPA=90°时,此时P和C重合,当∠ABP=90°时,求出AP的长即可.
解答:解:(1)如图1,
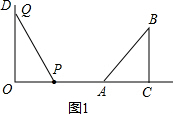
设点Q的运动速度为xcm/s,则OQ=xtcm,OP=t•1=t(cm),
∵Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,
∴由勾股定理得:AC=4cm,
∵∠BCA=∠QOP=90°,
∴要使△ABC与△POQ全等,
或
,
解得:x=
或
,
故答案为:
或
;
(2)根据题意得:有两种情况:当∠BPA=90°时,此时P和C重合,如图2,
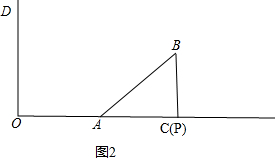
此时t=8+4=12;
当∠ABP=90°时,如图3,
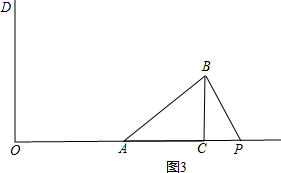
∵∠ABP=∠ACB=90°,∠BAC=∠BAP,
∴△BAC∽△PAB,
∴
=
,
∴
=
,
∴AP=
,
∴t=8+
=
,
所以当t=12秒或
秒时,△ABP是直角三角形.

设点Q的运动速度为xcm/s,则OQ=xtcm,OP=t•1=t(cm),
∵Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,
∴由勾股定理得:AC=4cm,
∵∠BCA=∠QOP=90°,
∴要使△ABC与△POQ全等,
|
|
解得:x=
| 4 |
| 3 |
| 3 |
| 4 |
故答案为:
| 4 |
| 3 |
| 3 |
| 4 |
(2)根据题意得:有两种情况:当∠BPA=90°时,此时P和C重合,如图2,

此时t=8+4=12;
当∠ABP=90°时,如图3,

∵∠ABP=∠ACB=90°,∠BAC=∠BAP,
∴△BAC∽△PAB,
∴
| AB |
| AP |
| AC |
| AB |
∴
| 5 |
| AP |
| 3 |
| 5 |
∴AP=
| 25 |
| 3 |
∴t=8+
| 25 |
| 3 |
| 49 |
| 3 |
所以当t=12秒或
| 49 |
| 3 |
点评:本题考查了勾股定理,相似三角形的性质和判定的应用,注意要进行分类讨论,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

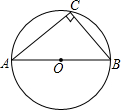 如图,△ABC内接于⊙O,AB为⊙O的直径,BC=6,AC=8.
如图,△ABC内接于⊙O,AB为⊙O的直径,BC=6,AC=8.