Question

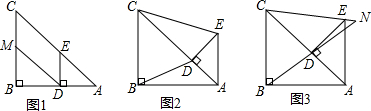
如图，在△ABC中，AB=BC，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结DE、DC、AE并延长AE交CD于F．
①说明AE=CD；
②若∠CAE=20°，求∠CDE的度数；
③猜想AF与CD的位置关系，并说明理由？

Answer 1

考点：全等三角形的判定与性质

专题：

分析：①首先利用SAS证明△ABE≌△CBD，再由全等三角形的性质即可得到AE=CD；
②由等腰直角三角形的性质可求出∠BAE的度数，再利用外角和定理即可确定出∠EDC的度数；
③要证明AF⊥CD，利用已知条件证明∠AFC=90°即可．

解答：①证明：在△ABE和△CBD中，

AB=CB ∠ABC=∠CBD=90° BE=BD

，
∴△ABE≌△CBD（SAS），
∴AE=CD；
②解：∵AB=BC，∠ABC=90°，
∴∠BAC=∠BCA=45°，
∵∠CAE=20°，
∴∠BAE=∠BDC=45°-20°=25°，
∴∠AEB=65°，
∴∠EDC=65°-25°=40°；
③AF⊥DC，理由如下：
∵△ABE≌△CBD，
∴∠BAE=∠BCD，
∵∠BAE+∠AEB=90°，
∴∠BCD+∠CEF=90°，
∴∠EFC=90°，
即AF⊥DC．

点评：此题考查了全等三角形的判定与性质，等腰直角三角形的性质以及三角形的外角性质，熟练掌握全等三角形的判定与性质是解本题的关键．