题目内容
14．若x+y=6，xy=4，且x＞y，则代数式$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$的值为$\frac{\sqrt{5}}{5}$．分析 先分母有理化，再代入计算即可．
解答 解：∵x+y=6，xy=4，且x＞y，
∴（x-y）2=（x+y）2-4xy=36-16=20，
∴x-y=2$\sqrt{5}$，
原式=$\frac{（\sqrt{x}-\sqrt{y}）^{2}}{（\sqrt{x}+\sqrt{y}）（\sqrt{x}-\sqrt{y}）}$
=$\frac{x+y-2\sqrt{xy}}{x-y}$
=$\frac{6-2\sqrt{4}}{2\sqrt{5}}$
=$\frac{\sqrt{5}}{5}$，
故答案为$\frac{\sqrt{5}}{5}$．
点评 本题考查了分母有理化，掌握完全平方公式的变形以及有理化因式是解题的关键．
练习册系列答案
相关题目
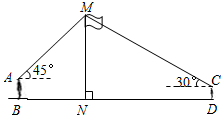如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离AB=1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离CD=1.5m，看旗杆顶部M的仰角为30°．两人相距28米且位于旗杆两侧（点B、N、D在同一条直线上）．请求出旗杆MN的高度．（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，结果保留整数）
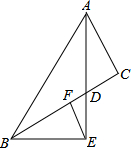如图，△ABC中，AD是角平分线，BE⊥AD，垂足E在AD延长线上，F是BC的中点，AB=30cm，AC=18cm．则EF的长为6cm．