题目内容
1.抛物线y=$\frac{1}{4}$x2+bx+c经过点(-1,0)和(3,0).(1)求该抛物线的解析式及顶点A的坐标.
(2)当-3<x<3时,使y=m成立的x的值恰好只有一个,求m的值或取值范围.
(3)平移图1中抛物线,使它过原抛物线顶点A,设平移后的抛物线顶点为B,对称轴交原抛物线于点D,点C是点A关于直线BD的对称点.平移后的位置如图2,若四边形ABCD的面积为4,求点B的坐标.
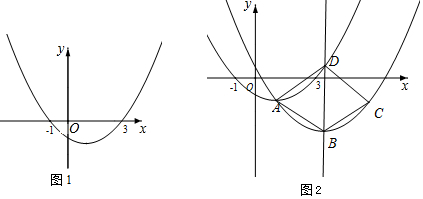
分析 (1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据自变量与函数值的对应关系,可得函数值的取值范围,可得答案.
(3)根据平移规律,可得新抛物线,根据待定系数法,可得b与a的关系,根据函数值相等点关于对称轴对称,可得C点坐标,根据对角线互相垂直的四边形的面积等于对角线乘积的一半,可得答案.
解答 解:(1)将(-1,0)和(3,0)代入函数解析式,得
$\left\{\begin{array}{l}{\frac{1}{4}-b+c=0}\\{\frac{1}{4}×9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{1}{2}}\\{c=-\frac{3}{4}}\end{array}\right.$,
∴y=$\frac{1}{4}$x2-$\frac{1}{2}$x-$\frac{3}{4}$.
配方,得y=$\frac{1}{4}$(x-1)2-1,
顶点A(1,-1).
(2)当x=-3时,y=3;当x=3时,y=0.
由图象 得,
得,
直线y=m与抛物线恰只有一个交点时,m=-1 或0≤m<3.
(3)设抛物线向右平移a个单位,向上平移b个单位,平移后的抛物线解析式:
y=$\frac{1}{4}$(x-1-a)2-1+b
∵抛物线过点A(1,-1),把A(1,-1)代入y=$\frac{1}{4}$(x-1-a)2-1+b,
得b=-$\frac{1}{4}$a2.
∴B(1+a,-1-$\frac{1}{4}$a2,D(1+a,$\frac{1}{4}$a2-1),C(1+2a,-1)
∴BD=$\frac{1}{2}$a2,AC=2a,
∵四边形ABCD的面积为4,
∴$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2a×$\frac{1}{2}$a2=4,
解得a=2.
1+a=3,-1-$\frac{1}{4}$a2=-2,
∴B(3,-2).
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法,解(2)的关键利用图象间的关系;解(3)的关键是利用对角线互相垂直的四边形的面积等于对角线乘积的一半得出关于a的方程.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案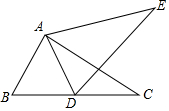 如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )
如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 65° |
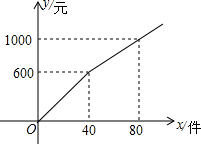 梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 15元 | C. | 12.5元 | D. | 10元 |
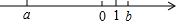 在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )
在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )| A. | |a|<1 | B. | |a|>1 | C. | |b|<1 | D. | ab>0 |
 如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )
如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
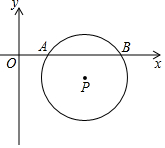 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2$\sqrt{3}$.将⊙P向上平移,当⊙P与x轴相切时平移的距离是( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2$\sqrt{3}$.将⊙P向上平移,当⊙P与x轴相切时平移的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
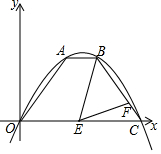 如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.