题目内容
9.化简:(-x$\sqrt{\frac{b}{a}}$)(-$\frac{a}{x}$$\sqrt{ax}$)(-2ab$\sqrt{\frac{x}{b}}$)(x>0).分析 根据二次根式的性质即可求出答案.
解答 解:当x>0时,
原式=a$\sqrt{bx}$•(-2ab$\sqrt{\frac{x}{b}}$)
=-2a2b$\sqrt{{x}^{2}}$
=-2a2bx
点评 本题考查二次根式的乘除法,解题的关键是书熟练运用二次根式的运算法则,本题属于基础题型.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
16.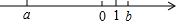 在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )
在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )
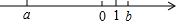 在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )
在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )| A. | |a|<1 | B. | |a|>1 | C. | |b|<1 | D. | ab>0 |
17.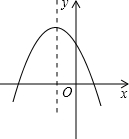 已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论:
①a<0,②b<0,③c<0,
其中正确的判断是( )
 已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论:①a<0,②b<0,③c<0,
其中正确的判断是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
14.下列四个几何体中,已知某个几何体的主视图、左视图、俯视图分别为圆、长方形、长方形,则该几何体是( )
| A. | 圆锥体 | B. | 圆柱体 | C. | 球体 | D. | 长方体 |
18.某学校初、高中六个年级共有3000名学生,为了解其视力情况,现采用抽样调查,各年级人数如下表所示:
(1)如果按10%的比例抽样,样本是什么?样本容量是多少?
(2)考虑到不同年级学生的视力差异,为了保证样本有较好的代表性,各年级分别应调查多少人?将结果填写在上面的表中;
(3)如果要从你所在的班50名学生中抽取5人进行调查,请设计一个抽样方案,保证每人有相同的机会被抽到.
| 年级 | 七年级 | 八年级 | 九年级 | 高一 | 高二 | 高三 | 合计 |
| 人数/名 | 560 | 520 | 500 | 500 | 480 | 440 | 3000 |
| 调查数/名 | 56 | 52 | 50 | 50 | 48 | 44 | 300 |
(2)考虑到不同年级学生的视力差异,为了保证样本有较好的代表性,各年级分别应调查多少人?将结果填写在上面的表中;
(3)如果要从你所在的班50名学生中抽取5人进行调查,请设计一个抽样方案,保证每人有相同的机会被抽到.