Question

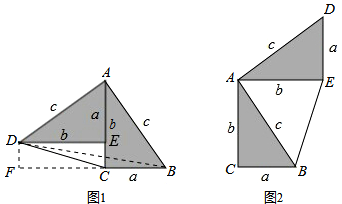
4．如图，在Rt△ACD中，∠ADC=90°，BE⊥AC于点E，交CD于点F，若AF平分∠CAD，线段FB和FC相等吗？请说明理由．

Answer 1

分析 根据角平分线性质可得EF=DF，即可求得△BDF≌△CEF即可解题．

解答 解：∵∠ADC=90°，BE⊥AC于点E，
∵AF平分∠BAC，
∴EF=DF，
在△BDF和△CEF中，
$\left\{\begin{array}{l}{∠DFB=∠EFC}\\{DF=EF}\\{∠BDF=CEF}\end{array}\right.$，
∴△BDF≌△CEF（ASA），
∴BF=FC．

点评 本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△BDF≌△CEF是解题的关键．