题目内容
14.化简或计算:(1)$\frac{b}{a-b}$+$\frac{a}{a+b}$+$\frac{2ab}{{a}^{2}-{b}^{2}}$
(2)($\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$)÷$\frac{x}{x-1}$
(3)$\sqrt{12}$-$\sqrt{18}$-$\sqrt{0.5}$+$\sqrt{\frac{1}{3}}$;
(4)$\frac{1}{3}$$\sqrt{{x}^{2}y}$×(-$\frac{1}{4}$$\sqrt{\frac{{y}^{2}}{x}}$)÷(-$\frac{1}{6}$$\sqrt{{x}^{2}}y$)
(5)解方程:$\frac{1}{x-3}$+2=$\frac{x-4}{3-x}$.
(6)解方程:$\frac{1}{y-1}$+$\frac{2}{{y}^{2}+2y-3}$=$\frac{y-1}{{y}^{2}-9}$.
分析 (1)先进行通分,再进行同分母的加法运算,然后把分子分解因式后约分即可;
(2)先把括号内通分和除法运算化为乘法运算,然后计算括号的同分母的加法运算,然后约分即可;
(3)先把各二次根式化为最简二次根式,然后合并即可;
(4)根据二次根式的乘法法则运算;
(5)先把方程化为整式方程得1+2(x-3)=-(x-4),然后解整式方程,最后进行检验确定原方程的解;
(6)先去分母,把原方程转化为整式方程(y+3)(y-3)+2(y-3)=(y-1)2,然后解整式方程,最后进行检验确定原方程的解.
解答 解:(1)原式=$\frac{b(a+b)}{(a+b)(a-b)}$+$\frac{a(a-b)}{(a+b)(a-b)}$+$\frac{2ab}{(a+b)(a-b)}$
=$\frac{{a}^{2}-2ab+{b}^{2}}{(a+b)(a-b)}$
=$\frac{(a-b)^{2}}{(a+b)(a-b)}$
=$\frac{a-b}{a+b}$;
(2)原式=[$\frac{(x+1)(x-1)}{(x-1)^{2}}$+$\frac{1}{(x-1)^{2}}$]•$\frac{x-1}{x}$
=$\frac{{x}^{2}}{(x-1)^{2}}$•$\frac{x-1}{x}$
=$\frac{x}{x-1}$;
(3)原式=2$\sqrt{3}$-3$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{3}$
=$\frac{7\sqrt{3}}{3}$-$\frac{7\sqrt{2}}{2}$;
(4)原式=$\frac{1}{3}$×(-$\frac{1}{4}$)×(-6)×$\sqrt{{x}^{2}y•\frac{{y}^{2}}{x}•\frac{1}{{x}^{2}y}}$
=$\frac{y\sqrt{x}}{2x}$;
(5)去分母得1+2(x-3)=-(x-4),
解得x=3,
经检验x=3是原方程的增根,
所以原方程无解;
(6)$\frac{1}{y-1}$+$\frac{2}{(y+3)(y-1)}$=$\frac{y-1}{(y+3)(y-3)}$,
方程两边同乘以(y-1)(y+3)(y-3)得(y+3)(y-3)+2(y-3)=(y-1)2,
解得y=4,
经检验y=4是原方程的解,
所以原方程的解为y=4.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了分式的混合运算和解分式方程.

 如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )| A. | 5050m2 | B. | 5000m2 | C. | 4900m2 | D. | 4998m2 |
 如图,在Rt△ACD中,∠ADC=90°,BE⊥AC于点E,交CD于点F,若AF平分∠CAD,线段FB和FC相等吗?请说明理由.
如图,在Rt△ACD中,∠ADC=90°,BE⊥AC于点E,交CD于点F,若AF平分∠CAD,线段FB和FC相等吗?请说明理由.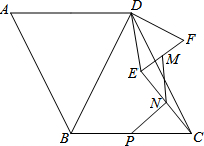 在?ABCD中,∠A=∠DBC,过点D作DE=DF,且∠EDF=∠ABD,连接EF、EC,M、N、P分别为EF、EC、BC的中点,连接NP.请你发现∠ABD与∠MNP满足的等量关系,并证明.
在?ABCD中,∠A=∠DBC,过点D作DE=DF,且∠EDF=∠ABD,连接EF、EC,M、N、P分别为EF、EC、BC的中点,连接NP.请你发现∠ABD与∠MNP满足的等量关系,并证明.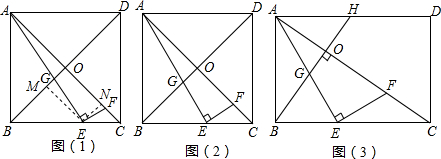
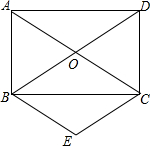 已知,如图,矩形ABCD的对角线AC,BD相交于点O,BE∥AC,CE∥DB.
已知,如图,矩形ABCD的对角线AC,BD相交于点O,BE∥AC,CE∥DB.