题目内容
20. 如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.(1)求点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.
分析 (1)由A、B坐标得出AB=5,根据点C是点A关于点B的对称点知BC=AB=5,据此可得;
(2)根据S△BCD=$\frac{1}{2}$BC•AD=10且BC=5,可得AD=4,即可知OP=2,据此可得答案.
解答 解:(1)∵点A(8,0),点B(3,0),
∴AB=5,
∵点C是点A关于点B的对称点,
∴BC=AB,
则点C的坐标为(-2,0);
(2)如图,
由题意知S△BCD=$\frac{1}{2}$BC•AD=10,BC=5,
∴AD=4,
则OP=2,
∴点P的坐标为(0,2)或(0,-2).
点评 本题主要考查坐标与图形的变化-对称,解题的关键是掌握对称的定义和性质.

练习册系列答案
相关题目
11.某个公司有15名工作人员,他们的月工资情况如表.则该公司所有工作人员的月工资的平均数、中位数和众数分别是( )
| 职务 | 经理 | 副经理 | 职员 |
| 人数 | 1 | 2 | 12 |
| 月工资(元) | 5 000 | 2 000 | 800 |
| A. | 520,2 000,2 000 | B. | 2 600,800,800 | C. | 1 240,2 000,800 | D. | 1 240,800,800 |
12.关于函数y=2x-3,下列结论正确的是( )
| A. | 图象必经过(0,-3) | B. | 图象不过第三象限 | ||
| C. | y随x的增大而减小 | D. | 当x>1.5时,y<0 |
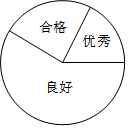 某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.
某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.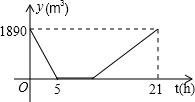 某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题: 如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B与∠D互余.
如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B与∠D互余.