题目内容
5.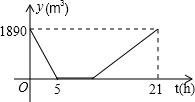 某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:(1)根据图中提供的信息,求排水的速度及清洗该游泳池所用的时间;
(2)求灌水过程中的y(m3)与换水时间t(h)之间的函数关系式,指出自变量t的取值范围.
分析 (1)根据函数图象和题意可以求得排水的速度及清洗该游泳池所用的时间;
(2)根据题意可以设出水过程中的y(m3)与换水时间t(h)之间的函数关系式,然后根据图象可以求得相应的函数解析式并写出自变量t的取值范围.
解答 解:(1)由题意可得,
排水速度是:1890÷5=378m3/h,
清洗游泳池的时间为:21-5-5×2=6h,
答:排水的速度是378m3/h,清洗游泳池的时间为6h;
(2)设灌水过程中的y(m3)与换水时间t(h)之间的函数关系式是y=kx+b,
由(1)知灌水对应的函数过点(11,0),(21,1890),
$\left\{\begin{array}{l}{11k+b=0}\\{21k+b=1890}\end{array}\right.$,得$\left\{\begin{array}{l}{k=189}\\{b=-2079}\end{array}\right.$,
答:灌水过程中的y(m3)与换水时间t(h)之间的函数关系式是y=189t-2079(11≤t≤21).
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想解答.

练习册系列答案
相关题目
15.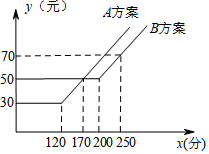 如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
 如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )| A. | 若通话时间少于120分,则A方案比B方案便宜20元 | |
| B. | 若通讯费用为60元,则B方案比A方案的通话时间多 | |
| C. | 若两种方案通讯费用相差10元,则通话时间是145分或185分 | |
| D. | 若通话时间超过200分,则B方案比A方案便宜12元 |
16.已知多项式A与2x2+5x的和等于2x2-3x+1,则这个多项式为( )
| A. | 2x-1 | B. | 2x+1 | C. | -8x+1 | D. | -8x-1 |
17.在下列代数式中,次数为3的单项式是( )
| A. | 3x2 | B. | -x2y | C. | x3+1 | D. | x3y |

 如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.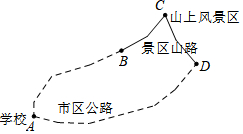 为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?
为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?