题目内容
2.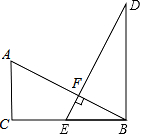 在△ABC中和△DBE中,∠ACB=∠DBC=90°,E是BC的中点,EF⊥AB于F,且AB=DE.
在△ABC中和△DBE中,∠ACB=∠DBC=90°,E是BC的中点,EF⊥AB于F,且AB=DE.(1)观察并猜想,BD、CE与AC有何数量关系?并证明你猜想的结论.
(2)若BD=8cm,试求△ABC的面积.
分析 (1)利用同角的余角相等求出∠A=∠FEB,再利用“角角边”证明△ACB和△EBD全等,根据全等三角形对应边相等可得BD=BC,AC=BE,然后根据BC=CE+BE等量代换证明即可;
(2)根据全等三角形对应边相等求出BC,根据线段中点的定义求出BE,从而得到AC,然后利用三角形的面积公式列式计算即可得解.
解答 (1)BD=CE+AC
证明:∵EF⊥AB,
∴∠EFB=90°,
∵∠ACB=90°,
∴∠A+∠ABC=90°,∠FEB+∠ABC=90°,
∴∠A=∠FEB,
在△ACB和△EBD中,$\left\{\begin{array}{l}{∠A=∠FEB}\\{∠C=∠DBE=90°}\\{AB=DE}\end{array}\right.$,
∴△ACB≌△EBD(AAS),
∴BD=BC,AC=BE,
∴BD=CE+AC;
(2)解:∵由(1)知:△ACB≌△EBD,
∴BC=BD=8cm,BE=AC,
∵E为BC中点,
∴BE=$\frac{1}{2}$BC=4cm,
即AC=4cm,
S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$×8×4=16cm2.
点评 本题考查了全等三角形的判定与性质,三角形的面积,熟练掌握三角形全等的判断方法是解题的关键.

练习册系列答案
相关题目
12.下列关于中点的说法中,正确的是( )
| A. | 若C是线段AB上的一点,且AC+CB=AB,则点C是AB的中点 | |
| B. | 若平面上有线段AB和一点C,且AC=CB,则点C是线段AB的中点 | |
| C. | 若C是线段AB上的一点,且AC=2CB,则点C是AB的中点 | |
| D. | 若延长线段AC到B,且AC=CB,则点C是线段AB的中点 |
 如图,h与b相交于O点,若∠1=30°,则∠2的度数是150°,∠3的度数是30°.
如图,h与b相交于O点,若∠1=30°,则∠2的度数是150°,∠3的度数是30°.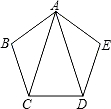 如图,在正五边形ABCDE中,AC、AD为对角线,则∠CAD的大小为36°.
如图,在正五边形ABCDE中,AC、AD为对角线,则∠CAD的大小为36°. 如图,已知点A、B、C.
如图,已知点A、B、C.