题目内容
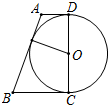如图，已知梯形ABCD中，AD∥BC，∠C=90°，以CD为直径的圆与AB相切，AB=6，那么梯形ABCD的面积是（ ）| A、2 | B、3 |
| C、4 | D、不能确定，与∠B的大小有关 |
考点：切线的性质
专题：
分析：根据切线长定理即可求得AD+BC=AB=6，而梯形ABCD的面积=
（AD+BC）•CD，AD+BC是定值，CD在AD、BC是定值的情况下，随∠B的变化而变化，故可以判定．
| 1 |
| 2 |
解答：解：∵AD∥BC，∠C=90°，
∴∠D=90°，
∴AD⊥DC，BC⊥DC，
∵CD为直径，
∴AD、BC是⊙O的切线，
∵以CD为直径的圆与AB相切，
∴AD+BC=AB=6，
而梯形ABCD的面积=
（AD+BC）•CD，
∵CD在AD、BC是定值的情况下，随∠B的变化而变化，
∴梯形ABCD的面积不能确定．
故选D．
∴∠D=90°，
∴AD⊥DC，BC⊥DC，
∵CD为直径，
∴AD、BC是⊙O的切线，
∵以CD为直径的圆与AB相切，
∴AD+BC=AB=6，
而梯形ABCD的面积=
| 1 |
| 2 |
∵CD在AD、BC是定值的情况下，随∠B的变化而变化，
∴梯形ABCD的面积不能确定．
故选D．
点评：本题考查了切线的判定和切线长定理，梯形的面积公式，熟练掌握性质和定理是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，四边形ABCD是菱形，对角线AC，BD相交于点O，BD=6，∠ACD=30°．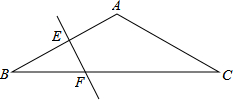
在△ABBC中，AB=AC，∠BAC=120°，EF为AB的垂直平分线，求证：BF=
如图，点A和点B分别是棱长为20cm的正方体盒子上两条棱的中点，一只昆虫沿盒子的表面由A处爬行到B处，所走的最短路程是多少？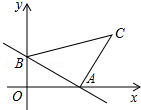
如图，一次函数y=-