题目内容
16.已知反比例函数$y=\frac{1-k}{x}$,当x<0时,y随x的增大而增大,则k的值可以是( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据反比例函数的性质列出关于k的不等式,求出k的取值范围即可.
解答 解:∵反比例函数$y=\frac{1-k}{x}$,当x<0时,y随x的增大而增大,
∴1-k<0,
解得k>1.
故选D.
点评 本题考查的是反比例函数的性质,即反比例函数y=$\frac{k}{x}$(k≠0)中,当k<0时,y随x的增大而增大.

练习册系列答案
相关题目
7.关于x的方程x2+2kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
8.若∠A、∠B为△ABC中的锐角,且$\sqrt{2sinA-\sqrt{3}}$+(cosB-$\frac{1}{2}$)2=0,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 无法确定 |
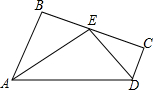 如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证:
如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证: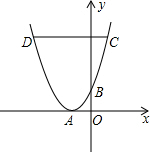 如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物线上一点,CD∥x轴交抛物线于点D.
如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物线上一点,CD∥x轴交抛物线于点D.