题目内容
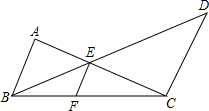 如图,已知AB∥EF∥CD,若AB=6cm,CD=9cm,BC=18cm,∠ABC=60°,求EF的长和△BCE的面积.
如图,已知AB∥EF∥CD,若AB=6cm,CD=9cm,BC=18cm,∠ABC=60°,求EF的长和△BCE的面积.考点:平行线分线段成比例,三角形的面积
专题:
分析:利用平行线分线段成比例可先求得BF,再求得EF;过E作EM⊥BC于M,可先求得EM,再求△BCE的面积.
解答: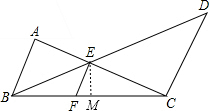 解:∵AB∥CD∥EF,
解:∵AB∥CD∥EF,
∴
=
=
,
即
=
=
,
∵BF+FC=BC=18cm,
∴BF=6,
又EF∥CD,
∴
=
即
=
,
∴EF=3,
过E作EM⊥BC于M,
∵EF∥AB,
∴∠EFC=∠ABC=60°,
∴EM=EFsin60°=3×
=
,
∴S△BCE=
BC•EM=
×18×
=
(cm2).
 解:∵AB∥CD∥EF,
解:∵AB∥CD∥EF,∴
| BF |
| FC |
| BE |
| ED |
| AB |
| CD |
即
| BF |
| FC |
| 6 |
| 9 |
| 2 |
| 3 |
∵BF+FC=BC=18cm,
∴BF=6,
又EF∥CD,
∴
| EF |
| CD |
| BF |
| BC |
即
| EF |
| 9 |
| 6 |
| 18 |
∴EF=3,
过E作EM⊥BC于M,
∵EF∥AB,
∴∠EFC=∠ABC=60°,
∴EM=EFsin60°=3×
| ||
| 2 |
3
| ||
| 2 |
∴S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
27
| ||
| 2 |
点评:本题主要考查平行线分线成比例的性质,掌握平行线分线段成比例中的线段对应成比例是解题的关键.

练习册系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图所示,小明与小王在公园游玩,小明在塔AC上的B处,小王在短墙DF的另一侧,小明的视线被短墙遮住.为了寻找小王,小明向上爬至塔顶C处.DF=4米,GE=6米,短墙底部D与塔的底部A间的距离为3米,小明从C点观察F点的俯角为53°,延长CF交DE于点G.若小王躲藏处M (点M在DE上)距D点2米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图所示,小明与小王在公园游玩,小明在塔AC上的B处,小王在短墙DF的另一侧,小明的视线被短墙遮住.为了寻找小王,小明向上爬至塔顶C处.DF=4米,GE=6米,短墙底部D与塔的底部A间的距离为3米,小明从C点观察F点的俯角为53°,延长CF交DE于点G.若小王躲藏处M (点M在DE上)距D点2米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)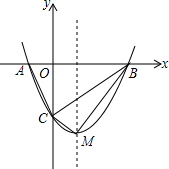 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.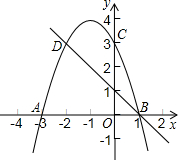 如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(-3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B、D两点.
如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(-3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B、D两点.