题目内容
15.小明在数学课外小组活动中遇到这样一个“新定义”问题:定义运算“※”为:a※b=$\left\{\begin{array}{l}{\frac{a}{b}(b>0)}\\{-\frac{a}{b}(b<0)}\end{array}\right.$,求1※(-4)的值.
小明是这样解决问题的:由新定义可知a=1,b=-4,又b<0,所以1※(-4)=$\frac{1}{4}$
请你参考小明的解题思路,回答下列问题:
(1)计算:3※7;
(2)若15※m=$\frac{15}{4}$,求m的值;
(3)函数y=4※x(x≠0)的图象大致是D
A.
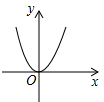 B.
B. C.
C.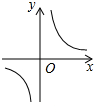 D.
D.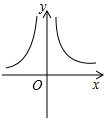
分析 (1)利用题中的新定义计算即可得到结果;
(2)分m大于0与小于0两种情况,利用题中的新定义计算即可求出m的值;
(3)分x大于0与x小于0两种情况化简函数解析式,做出函数图象即可.
解答 解:(1)根据题中的新定义得:3※7=$\frac{3}{7}$;
(2)当m>0时,已知等式变形得:$\frac{15}{m}$=$\frac{15}{4}$,即m=4;
当m<0时,已知等式变形得:-$\frac{15}{m}$=$\frac{15}{4}$,即m=-4;
(3)当x>0时,函数解析式为y=$\frac{4}{x}$,
当x<0时,函数解析式为y=-$\frac{4}{x}$,
图象大致为D.
故选:D.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )
如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )
 如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )
如图,△ABC是边长为6cm的等边三角形,点P是AC边上一动点,由点A向点C运动(不与点A,C重合),点Q是CB延长线上一动点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.则ED的长为( )| A. | 2cm | B. | 3cm | ||
| C. | 4cm | D. | 缺少条件,无法求出 |
6. 如图所示是某几何体的三视图,则该几何体的侧面积是( )
如图所示是某几何体的三视图,则该几何体的侧面积是( )
 如图所示是某几何体的三视图,则该几何体的侧面积是( )
如图所示是某几何体的三视图,则该几何体的侧面积是( )| A. | $\sqrt{10}$π | B. | 2$\sqrt{10}$π | C. | 3π | D. | 6π |
3.关于m的不等式-m>1的解为( )
| A. | m>0 | B. | m<0 | C. | m<-1 | D. | m>-1 |
4.若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )
| A. | (2,-3) | B. | (-2,-3) | C. | (2,3) | D. | (-1,-6) |
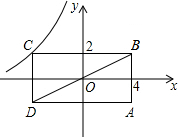 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{k}{x}$的图象上,若点A的坐标为(4,-2),则k的值为-8. 如图,EF∥BC,AC平分∠BAF,∠B=80°,则∠C=50°.
如图,EF∥BC,AC平分∠BAF,∠B=80°,则∠C=50°. 如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).
如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).