题目内容
9.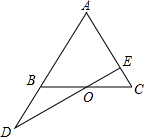 如图,已知点O是△ABC中BC边上的中点,且$\frac{BD}{AB}$=$\frac{3}{5}$,则$\frac{CE}{AE}$=$\frac{3}{8}$.
如图,已知点O是△ABC中BC边上的中点,且$\frac{BD}{AB}$=$\frac{3}{5}$,则$\frac{CE}{AE}$=$\frac{3}{8}$.
分析 过B作BF平行于AC,交DE于点F,由两直线平行内错角相等得到两对内错角相等,再由O为BC的中点,得到BO=CO,利用AAS可得出三角形BOF与三角形COE全等,根据全等三角形对应边相等可得出BF=EC,再由BF平行于AE,利用平行线等分线段定理列出比例式,然后根据已知条件即可得到结论.
解答 解:过B作BF∥AC,交DE于点F, ∵BF∥AC,
∵BF∥AC,
∴∠FBO=∠C,∠BFO=∠CEO,
又O为BC的中点,∴BO=CO,
在△OBF和△OCE中,
$\left\{\begin{array}{l}{∠FBO=∠C}\\{∠BFO=∠CEO}\\{BO=CO}\end{array}\right.$,
∴△OBF≌△OCE(AAS),
∴BF=CE,
∵$\frac{BD}{AB}$=$\frac{3}{5}$,
∴$\frac{BD}{AD}$=$\frac{3}{8}$.
∵BF∥AE,
∴△BDF∽△ADE,
∴$\frac{CE}{AE}$=$\frac{BD}{AD}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 此题考查了平行线分线段成比例性质,全等三角形的判定与性质,以及比例的性质,其中根据题意作出辅助线BF∥AC是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.一个长方形的宽是1.5×102cm,长是宽的6倍,则这个长方形的面积(用科学记数法表示)是( )
| A. | 13.5×104 cm2 | B. | 1.35×105 cm2 | C. | 1.35×104 cm2 | D. | 1.35×103 cm2 |
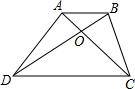 如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a<b),若△BOC的面积为梯形面积的$\frac{2}{9}$,则$\frac{a}{b}$=$\frac{1}{2}$. 如图,∠C=90°,∠1=∠2,若CD=4,则D到AB的距离为4.
如图,∠C=90°,∠1=∠2,若CD=4,则D到AB的距离为4.