题目内容
在Rt△ABC中，∠C=90°，BC=12cm，BC边上的中线AD=10cm，则sinB= ．
考点：勾股定理,锐角三角函数的定义
专题：
分析：首先在Rt△ACD中，利用勾股定理求得AC的长度；然后在Rt△ABC中，利用勾股定理求得AB的长度；最后利用锐角三角函数的定义进行解答．
解答：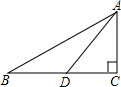
解：如图，∵BC=12cm，AD是BC边上的中线，
∴CD=
BC=6cm．
∴在Rt△ACD中，∠C=90°，CD=6cm，AD=10cm，
∴由勾股定理得 AC=
=
=8（cm）．
∴在Rt△ABC中，由勾股定理得 AB=
=
=4
（cm）．
∴sinB=
=
=
．
故答案是：
．
解：如图，∵BC=12cm，AD是BC边上的中线，∴CD=
| 1 |
| 2 |
∴在Rt△ACD中，∠C=90°，CD=6cm，AD=10cm，
∴由勾股定理得 AC=
| AD2-CD2 |
| 102-62 |
∴在Rt△ABC中，由勾股定理得 AB=
| AC2+BC2 |
| 82+122 |
| 13 |
∴sinB=
| AC |
| AB |
| 8 | ||
4
|
2
| ||
| 13 |
故答案是：
2
| ||
| 13 |
点评：本题考查了勾股定理和锐角三角函数的定义．解答此类问题的关键是分别设出AC、AB的长度．
练习册系列答案
相关题目
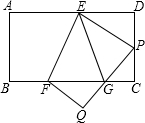已知矩形纸片ABCD中，AD=6，CD=4，将纸片折叠，使点A落在CD边上点P处（点P与C、D不重合），折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．
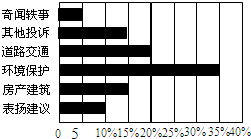如图是某晚报“百姓热线”一周内接到热线电话的统计图，其中有关环境保护问题的电话最多，共7 0个，请回答下列问题：