题目内容
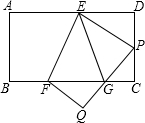 已知矩形纸片ABCD中,AD=6,CD=4,将纸片折叠,使点A落在CD边上点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
已知矩形纸片ABCD中,AD=6,CD=4,将纸片折叠,使点A落在CD边上点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.(1)当P位于CD边中点时,求△PCG与△EDP的相似比;
(2)在(1)的条件下,求FG的长.
考点:翻折变换(折叠问题),全等三角形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)根据翻折的性质可得AE=EP,设ED=x,表示出EP,再利用勾股定理列出方程求出x,然后根据相似三角形相似比的定义解答;
(2)求出CG,再利用勾股定理列式 求出PG,然后求出QG,从而得到CG=QG,再利用“角边角”证明△PCG和△FQG全等,根据全等三角形对应边相等可得FG=PG.
(2)求出CG,再利用勾股定理列式 求出PG,然后求出QG,从而得到CG=QG,再利用“角边角”证明△PCG和△FQG全等,根据全等三角形对应边相等可得FG=PG.
解答:解:(1)由翻折的性质的,AE=EP,
设ED=x,则EP=AE=6-x,
∵P位于CD边中点,
∴DP=CP=
CD=
×4=2,
在Rt△PDE中,ED2+DP2=EP2,
即x2+22=(6-x)2,
解得x=
,
所以,
=
=
,
即△PCG与△EDP的相似比为
;
(2)∵∠EPD+∠CPG=90°,
∠EPD+∠DEP=90°,
∴∠DEP=∠CPG,
又∵∠D=∠C=90°,
∴△PCG∽△EDP,
∴
=
=
,
∴CG=
DP=
×2=
,
在Rt△CGP中,由勾股定理得,DP=
=
,
∴QG=4-
=
,
∴CG=QG,
在△PCG和△FQG中,
,
∴△PCG≌△FQG(ASA),
∴FG=PG=
.
设ED=x,则EP=AE=6-x,
∵P位于CD边中点,
∴DP=CP=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PDE中,ED2+DP2=EP2,

即x2+22=(6-x)2,
解得x=
| 8 |
| 3 |
所以,
| PC |
| ED |
| 2 | ||
|
| 3 |
| 4 |
即△PCG与△EDP的相似比为
| 3 |
| 4 |
(2)∵∠EPD+∠CPG=90°,
∠EPD+∠DEP=90°,
∴∠DEP=∠CPG,
又∵∠D=∠C=90°,
∴△PCG∽△EDP,
∴
| DP |
| CG |
| PC |
| ED |
| 4 |
| 3 |
∴CG=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
在Rt△CGP中,由勾股定理得,DP=
22+(
|
| 5 |
| 2 |
∴QG=4-
| 5 |
| 2 |
| 3 |
| 2 |
∴CG=QG,
在△PCG和△FQG中,
|
∴△PCG≌△FQG(ASA),
∴FG=PG=
| 5 |
| 2 |
点评:本题考查了翻折变换的性质,勾股定理,相似三角形的性质,全等三角形的判定与性质,(1)利用勾股定理列方程求出ED的长是解题的关键,(2)根据线段的长度得到CG=QG是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 如图,△BDE是等边三角形,∠BDC=30°,∠ABD=∠ADB=15°,∠CBD=45°.求证:△ABC是等边三角形.
如图,△BDE是等边三角形,∠BDC=30°,∠ABD=∠ADB=15°,∠CBD=45°.求证:△ABC是等边三角形.