Question

15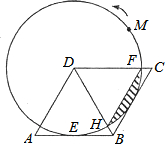．如图，在菱形ABCD中，AB=2$\sqrt{3}$，∠A=60°，以点D为圆心的⊙D与边AB相切于点E．
（1）求证：⊙D与边BC也相切；
（2）设⊙D与BD相交于点H，与边CD相交于点F，连接HF，求图中阴影部分的面积（结果保留π）．

Answer 1

分析 （1）作DG⊥BC于G，连结DE，如图，根据切线的性质得DE⊥AB，再根据菱形的性质得BD平分∠ADC，则根据角平分线的性质得DG=DE，然后根据切线的判断定理即可得到⊙D与边BC也相切；
（2）根据菱形的性质得DB=DC=AB=2$\sqrt{3}$，∠DCB=∠A=60°，则可判断△DBC为等边三角形，根据等边三角形的性质得∠BDC=60°，DG=$\frac{\sqrt{3}}{2}$BC=3，再利用DH=DF=DG=3得到△DHF为等边三角形，然后根据扇形面积公式，利用S_阴影部分=S_扇形HDF-S_△DHF进行计算即可．

解答 （1）证明：作DG⊥BC于G，连结DE，如图，
∵AB与⊙D相切于点E，
∴DE⊥AB，
∵四边形ABCD为菱形，
∴BD平分∠ADC，
而DE⊥AB，DG⊥BC，
∴DG=DE，
即DG为⊙D的半径，
∴⊙D与边BC也相切；
（2）解：∵在菱形ABCD中，AB=2$\sqrt{3}$，∠A=60°，
∴DB=DC=AB=2$\sqrt{3}$，∠DCB=∠A=60°，
∴△DBC为等边三角形，
∴∠BDC=60°，DG=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$×2$\sqrt{3}$=3，
∵DH=DF=DG=3，
∴△DHF为等边三角形，
∴S_阴影部分=S_扇形HDF-S_△DHF
=$\frac{60•π•{3}^{2}}{360}$-$\frac{\sqrt{3}}{4}$×3²
=$\frac{3}{2}$π-$\frac{9\sqrt{3}}{4}$．

点评 本题考查了切线的判定与性质：圆的切线垂直于经过切点的半径；经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了菱形的性质和扇形面积的计算．