题目内容
4．化简求值：$\frac{1}{x-1}$-$\frac{x+1}{{x}^{2}-1}$+$\frac{1}{x+1}$，其中x=-$\frac{1}{2}$．分析 先把要求的式子进行通分，再进行约分，最后把x的值代入计算即可得出答案．
解答 解：$\frac{1}{x-1}$-$\frac{x+1}{{x}^{2}-1}$+$\frac{1}{x+1}$=$\frac{x+1}{（x+1）（x-1）}$-$\frac{x+1}{（x+1）（x-1）}$+$\frac{x-1}{（x+1）（x-1）}$=$\frac{1}{x+1}$，
把x=-$\frac{1}{2}$代入上式得：
原式=$\frac{1}{-\frac{1}{2}+1}$=2．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
15．2016年9月28第七届安徽省花博会在阜阳开幕．开幕前夕，我市某工艺厂设计了一款成本为10元/件的柳编工艺品投放市场进行试销．阜阳市物价部门规定该工艺品销售单价不得低于成本价，最高不能超过38元/件，经过调查，得到如表数据：
（1）若y与x是一次函数关系y=kx+b，求这个一次函数关系式；
（2）当销售单价定为多少时，该厂试销该工艺品每天所获利润最大？最大利润是多少？
（3）若该工艺厂要获得的利润不低于8000元，试确定销售单价x的取值范围．
| 销售单价x（元/件） | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量（y件） | … | 500 | 400 | 300 | 200 | 100 | … |
（2）当销售单价定为多少时，该厂试销该工艺品每天所获利润最大？最大利润是多少？
（3）若该工艺厂要获得的利润不低于8000元，试确定销售单价x的取值范围．
9．
在数轴上点A、B对应的数为a、b，则a+b+3的和为（ ）
在数轴上点A、B对应的数为a、b，则a+b+3的和为（ ）| A． | 正数 | B． | 负数 | C． | 0 | D． | 不确定 |
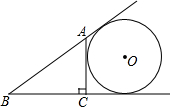如图，AC⊥BC于点C，⊙O与直线AB、BC、CA都相切，若BC=3，△ABC的周长是10，则⊙O的半径等于2．