题目内容
20.某地探空气球的气象观测资料表明,高度每增加1千米,气温大约降低6℃,若该地区地面温度为23℃,该地区高空某点温度为-37℃,求此点的高度是10千米.分析 根据题意列出算式,计算即可得到结果.
解答 解:根据题意得:[23-(-37)]÷6×1=10(千米),
则此点的高度是10千米,
故答案为:10
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.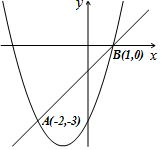 如图,二次函数y=ax2+bx+c(a≠0)和一次函数y=x-1的图象交于A(-2,-3)、B(1,0)两点,则方程ax2+(b-1)x+c+1=0的根为( )
如图,二次函数y=ax2+bx+c(a≠0)和一次函数y=x-1的图象交于A(-2,-3)、B(1,0)两点,则方程ax2+(b-1)x+c+1=0的根为( )
 如图,二次函数y=ax2+bx+c(a≠0)和一次函数y=x-1的图象交于A(-2,-3)、B(1,0)两点,则方程ax2+(b-1)x+c+1=0的根为( )
如图,二次函数y=ax2+bx+c(a≠0)和一次函数y=x-1的图象交于A(-2,-3)、B(1,0)两点,则方程ax2+(b-1)x+c+1=0的根为( )| A. | x1=-2,x2=-3 | B. | x1=1,x2=0 | C. | x1=-2,x2=1 | D. | x1=-3,x2=0 |
15.2016年9月28第七届安徽省花博会在阜阳开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的柳编工艺品投放市场进行试销.阜阳市物价部门规定该工艺品销售单价不得低于成本价,最高不能超过38元/件,经过调查,得到如表数据:
(1)若y与x是一次函数关系y=kx+b,求这个一次函数关系式;
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
9. 在数轴上点A、B对应的数为a、b,则a+b+3的和为( )
在数轴上点A、B对应的数为a、b,则a+b+3的和为( )
 在数轴上点A、B对应的数为a、b,则a+b+3的和为( )
在数轴上点A、B对应的数为a、b,则a+b+3的和为( )| A. | 正数 | B. | 负数 | C. | 0 | D. | 不确定 |
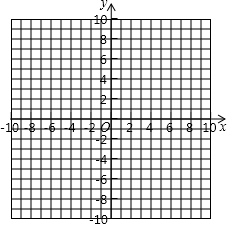 在如图的平面直角坐标系中作△ABC,使点A、B、C的坐标分别为A(4,6),B(0,2),C(6,0),并作出△ABC关于y轴的对称图形.
在如图的平面直角坐标系中作△ABC,使点A、B、C的坐标分别为A(4,6),B(0,2),C(6,0),并作出△ABC关于y轴的对称图形. 如图,AD是△ABC 的角平分线,DE⊥AB,AB=4,DE=2,S△ABC=7,则AC的长是3.
如图,AD是△ABC 的角平分线,DE⊥AB,AB=4,DE=2,S△ABC=7,则AC的长是3.