��Ŀ����
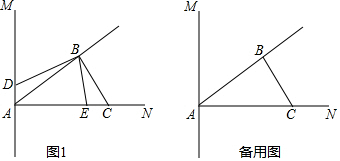
18����ͼ1��ֱ��AM��AN��ABƽ�֡�MAN������B��BC��BA��AN�ڵ�C������E��Dͬʱ��A����������ж���E��2m/s���ٶ�������AN�����˶�������D��1m/s���ٶ��˶�����֪AC=6 cm���趯��D��E���˶�ʱ��Ϊt����1�������ACB�Ķ�����
��2������D������AM���˶�ʱ����S��ADB��S��BEC=2��3�������D��E���˶�ʱ��t��ֵ��
��3��������D��ֱ��AM���˶���E������AN�˶������У��Ƿ����ij��ʱ��t��ʹ�á�ADB���BECȫ�ȣ������ڣ������ʱ��t��ֵ���������ڣ���˵�����ɣ�
���� ��1�����ݽ�ƽ���ߵĶ��塢ֱ�������ε���ǻ��༴�ɽ�����⣮
��2����BH��AC��H��BG��AM��G����BAƽ�֡�MAN���Ƴ�BG=BH����S��ADB��S��BEC=2��3��AD=t��AE=2t���ɵ�$\frac{1}{2}$•t•BG��$\frac{1}{2}$•��6-2t��•BH=2��3���ⷽ�̼��ɽ�����⣮
��3�����ڣ���BA=BC����BAD=��BCE=45�㣬��֪��AD=ECʱ����ADB�ա�CEB���г����̼��ɽ�����⣮
��� �⣺��1����ͼ1�У�
��AM��AN��
���MAN=90�㣬
��ABƽ�֡�MAN��
���BAC=45�㣬
��CB��AB��
���ABC=90�㣬
���ACB=45�㣮
��2����ͼ2�У�
��BH��AC��H��BG��AM��G��
��BAƽ�֡�MAN��
��BG=BH��
��S��ADB��S��BEC=2��3��AD=t��AE=2t��
��$\frac{1}{2}$•t•BG��$\frac{1}{2}$•��6-2t��•BH=2��3��
��t=$\frac{12}{7}$s��
�൱t=$\frac{12}{7}$sʱ������S��ADB��S��BEC=2��3��
��3�����ڣ���BA=BC����BAD=��BCE=45�㣬
�൱AD=ECʱ����ADB�ա�CEB��
��t=6-2t��
��t=2s��
��t=2sʱ����ADB�ա�CEB��
���� ���⿼���������ۺ��⡢����ֱ�������ε����ʡ�ȫ�������ε��ж������ʡ������ε������֪ʶ������Ĺؼ���ѧ�ṹ�����̽�����⣬�����п��������ͣ�

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� �߽�������ϵ�д�
�߽�������ϵ�д�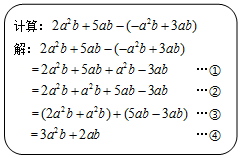
| A�� | �٣�ȥ���ŷ��� | B�� | �ڣ��ӷ������� | ||
| C�� | �ۣ���ʽ�Ļ������� | D�� | �ܣ��ϲ�ͬ����� |
 ������н�����̲�����������������ע�����ɣ���ͼ��EF��AD����1=��2����BAC=80�㣬���AGD��
������н�����̲�����������������ע�����ɣ���ͼ��EF��AD����1=��2����BAC=80�㣬���AGD��