题目内容
9.已知A=2x2+3xy-2x-1,B=x2+xy-1,且3A+6B的值与x无关,则y=$\frac{2-4x}{5}$.分析 先求出3A+6B,然后将含x的项进行合并即可求出y的值.
解答 解:3A+6B=3(2x2+3xy-2x-1)+6(x2+xy-1)
=6x2+9xy-6x-3+6x2+6xy-6
=12x2+15xy-6x-9
=12x2+(15y-6)x-9
由于3A+6B与x的值无关,
∴12x2+(15y-6)x=0,
∴y=$\frac{2-4x}{5}$
故答案为:$\frac{2-4x}{5}$
点评 本题考查整式的加减运算,解题的关键是将3A+6B进行化简,然后列出等式求出y的值,本题属于基础题型.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
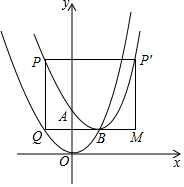 如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).
如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).