题目内容
3. 已知:抛物线C1:y=(x+1)2+1
已知:抛物线C1:y=(x+1)2+1(1)抛物线C1的顶点A的坐标(-1,1),它与y轴交点B的坐标是0,2).
(2)在平面直角坐标系中画出C1的图象(不必列表).
(3)画出C1平移后的图象C2,使点B平移到点C(2,0)的位置,平移后的抛物线C2的顶点为D.
(4)连结BC,AD,直接写出C1上A,B两点之间的部分平移至D,C两点之间时扫过的面积4.
分析 (1)根据顶点式即可求得;
(2)利用五点法画出图象即可;
(3)画出平移后的图象,根据图象即可得到平移方向和距离,从而求得顶点D的坐标;
(4)根据图象求得即可.
解答 解:(1)∵抛物线C1:y=(x+1)2+1,
∴顶点A的坐标为(-1,1),
令x=0,则y=2
∴与y轴的交点为(0,2);
故答案为(-1,1),(0,2);
(2)画出C1的图象如图: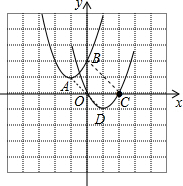
(3)如上图,
∵B(0,2),C(2,0),
∴B点向下平移2个单位,向右平移2个单位得到C,
∴平移后的顶点D的坐标为(1,-1);
(4)根据图象即可求得A,B两点之间的部分平移至D,C两点之间时扫过的面积为4.
故答案为4.
点评 本题考查了二次函数的图象,以及二次函数图象与几何变换,求得D点的坐标是解题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
3.下列各组数中,能够构成直角形三边的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 3,4,6 | C. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ | D. | $\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$ |
18.下列方程是关于x的一元二次方程的是( )
| A. | x2=1 | B. | x+$\frac{1}{x}$=1 | C. | x+2y=1 | D. | x(x-1)=x2 |
8.下列计算不正确的是( )
| A. | (-3)0=-1 | B. | 3.8×10-5=0.000038 | ||
| C. | 20020=20030 | D. | ($\frac{1}{4}$)-2=16 |
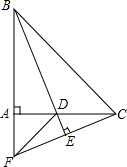 已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.
已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.