题目内容
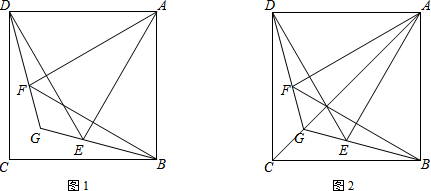
10.已知矩形ABCD.如图1,以AD、AB为边向内作等边△ADE和等边△ABF,延长DF、BE相交于点G.(1)求证:DF=BE.
(2)猜想∠EGF的度数,并说明理由.
(3)如图2,当点G位于对角线AC上时,
①求证:∠DGA=∠BGA;
②直接写出GE与BE的数量关系.
分析 (1)由等边三角形的性质可证明△ADF≌△AEB,可证明DF=BE;
(2)由(1)证明△ADF≌△AEB,结合三角形外角的性质可得到∠DEA+∠AEB=∠GDE+∠EGF,整理可得到∠EGF=120°;
(3)①过点A作AM⊥DG,AN⊥BG于点M、N,可证得△AMF≌△ABN,可得AM=AN,根据角平分线的判定可知∠DGA=∠BGA;
②连接EF,可证得EF=BE,在Rt△GEH中,利用三角函数的定义可求得sin60°=$\frac{EH}{GE}$,可证得结论.
解答 (1)证明:∵△ADE与△ABF均为等边三角形,
∴AD=AE,AF=AB,且∠DAF+∠FAE=∠BAE+∠FAE=60°,
∴∠DAF=∠BAE,
在△ADF和△AEB中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAF=∠BAE}\\{AF=AB}\end{array}\right.$,
∴△ADF≌△AEB(SAS),
∴DF=BE;
(2)解:猜想∠EGF=120°.
理由如下:∵△ADF≌△AEB,
∴∠AEB=∠ADF=∠GDE+∠ADE=∠GDE+60°,
又∵∠DEB=∠GDE+∠EGF,
即∠DEA+∠AEB=∠GDE+∠EGF,
∴60°+∠GDE+60°=∠GDE+∠EGF,
∴∠EGF=120°;
(3)①证明:如图1,过点A作AM⊥DG,AN⊥BG于点M、N,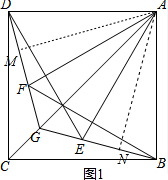
∵△ADF≌△ABE(已证),
∴∠DFA=∠EBA,AF=AB,
且∠FMA=∠BNA=90°,
在△AMF和△ABN中,
$\left\{\begin{array}{l}{∠DFA=∠EBN}\\{∠FMA=∠BNA}\\{AF=AB}\end{array}\right.$,
∴△AMF≌△ABN(AAS),
∴AM=AN,
∵∠FMA=∠BNA=90°,
∴∠DGA=∠BGA;
②解:BE=$\sqrt{3}$GE.
理由如下:
如图2,连接EF,
由题意可知AE垂直平分BF,所以EF=BE,
又∵∠EGF=120°,∠DGA=∠BGA(已证)
∴∠BGA=60°,
由条件又可证EF⊥AC于点H,可得EH=FH,
在Rt△GEH中,sin∠AGE=$\frac{EH}{GE}$,即sin60°=$\frac{EH}{GE}$,
∴2EH=$\sqrt{3}$GE,即BE=$\sqrt{3}$GE.
点评 本题主要考查矩形的性质和全等三角形的判定和性质、等边三角形的性质、角平分线的判定和三角函数的定义等知识点的综合应用.在(1)中求得∠DAF=∠BAE,证明三角形全等是解题的关键;在(2)中利用全等三角形的性质和三角形的外角的性质得到∠DEA+∠AEB=∠GDE+∠EGF是解题的关键;在(3)①中利用三角形全等证明AM=AN是解题的关键,在②中利用三角函数的定义找到EH和GE的关系是解题的关键.本题知识点较多,综合性较强,难度较大.

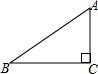 如图,在△ABC中,∠C=90°,AB=3,BC=2,则cosB的值是( )
如图,在△ABC中,∠C=90°,AB=3,BC=2,则cosB的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
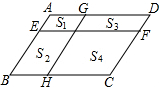 如图,EF和GH将?ABCD分成四个小平行四边形,设面积分别为S1=1,S2=3,S3=4,那么S4等于( )
如图,EF和GH将?ABCD分成四个小平行四边形,设面积分别为S1=1,S2=3,S3=4,那么S4等于( ) 解不等式组$\left\{\begin{array}{l}{5x-2>3x}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$,并把它的解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}{5x-2>3x}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$,并把它的解集表示在数轴上.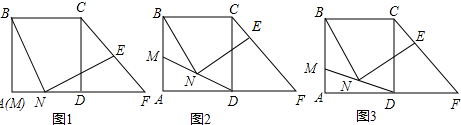
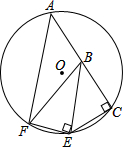 如图,AC为⊙O的弦,CE⊥AC交⊙O于E,B为AC上的一点,BC=CE,EF⊥BE交⊙O于F,⊙O的直径为13,BE=5$\sqrt{2}$.
如图,AC为⊙O的弦,CE⊥AC交⊙O于E,B为AC上的一点,BC=CE,EF⊥BE交⊙O于F,⊙O的直径为13,BE=5$\sqrt{2}$.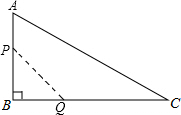 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.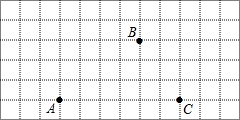 如图,A、B、C是网格图中的三点.
如图,A、B、C是网格图中的三点.