题目内容
20.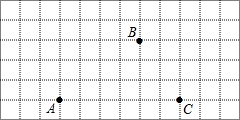 如图,A、B、C是网格图中的三点.
如图,A、B、C是网格图中的三点.(1)作直线AB、射线AC、线段BC.
(2)过B作AC的平行线BD.
(3)作出表示B到AC的距离的线段BE.
(4)判断BD与BE的位置关系是垂直.
(5)线段BE与BC的大小关系是:BE<BC(填“>”、“<”、“=”).
分析 (1)根据直线是向两方无限延伸的;射线是向一方无限延伸;线段本身不能向两方无限延伸画图即可;
(2)根据网格画平行线的即可;
(3)过B作BE⊥AC,BE长就是B到AC的距离;
(4)根据两直线平行内错角相等可得BD⊥BE;
(5)根据垂线段最短可得答案.
解答  解:(1)(2)(3)如图所示:
解:(1)(2)(3)如图所示:
(4)BD与BE的位置关系是垂直,
∵BE⊥AC,
∴∠BEC=90°,
∵DB∥AC,
∴∠DBE=∠BEC=90°,
∴BD⊥BE;
故答案为:垂直;
(5)根据垂线段最短可得BE<CB.
故答案为:<.
点评 此题主要考查了基本作图,关键是掌握两直线平行内错角相等,垂线段最短,以及直线、射线、线段的性质.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
11.已知$\frac{1}{x}-\frac{1}{y}=2$,则$\frac{2}{y^2}+\frac{2y-4x}{{{x^2}y}}$的值是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 8 | D. | $\frac{1}{8}$ |
8. 如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
 如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )| A. | 新 | B. | 年 | C. | 祝 | D. | 乐 |
15. 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )
 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )| A. | -3 | B. | -2 | C. | -2.5 | D. | -3.5 |
5.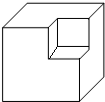 从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
 从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )| A. | 4a3 | B. | 8a3 | C. | 56a3 | D. | 58a3 |
 如图,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,若BD=3,则DE=3.
如图,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,若BD=3,则DE=3. ,答案显示此方程的解是x=3,若被墨水遮盖的是一个常数,则这个常数是4.
,答案显示此方程的解是x=3,若被墨水遮盖的是一个常数,则这个常数是4.