题目内容
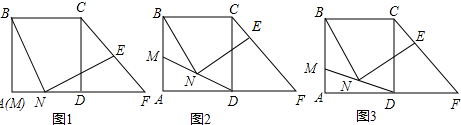
5.在正方形ABCD中,点F在AD延长线上,且DF=DC,M为AB边上一点,N为MD的中点,点E在线段CF上(点E与点C不重合).(1)如图1,若点M、A重合,E为CF的中点,试求tan∠ENF的值;
(2)如图2,若点M、A不重合,BN=NE,求证:BN⊥NE;
(3)如图3,在(2)的条件下,当$\frac{CE}{EF}=\frac{1}{2}$,求tan∠ADM的值.
分析 (1)作EG∥CD于G,证明DN=DG=EF=EG,即可得出tan∠ENF的值;
(2)延长BN交CD的延长线于G,作EH⊥CE交CD于H;先证明GN=BN,再证明NE=BN=GN=$\frac{1}{2}$BG,得出∠BEG=90°,然后证明BCE≌△GHE,得出BE=GE,即可得出结论;
(3)设CE=a,则EF=2a,CF=3a,根据题意求出AD、AM即可得出结果.
解答 (1)解:作EG∥CD于G,如图1所示: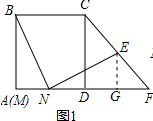 ∵E为CF的中点,
∵E为CF的中点,
∴DG=FG=$\frac{1}{2}$DF,EG=$\frac{1}{2}$CD,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵DF=DC,
∴AD=DF,
∵N为MD的中点,
∴DN=$\frac{1}{2}$AD,
∴DN=DG=EF=EG,
∴tan∠ENF=$\frac{EG}{NG}$=$\frac{1}{2}$;
(2)证明:延长BN交CD的延长线于G,作EH⊥CE交CD于H;如图2所示: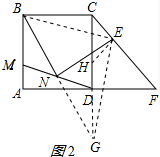
∵N为MD的中点,
∴DN=MN,
∵AB∥CG,
∴$\frac{GN}{BN}=\frac{DN}{MN}$=1,
∴GN=BN,
∵BN=NE,
∴NE=BN=GN=$\frac{1}{2}$BG,
∴∠BEG=90°,
∵EH⊥CE,
∴∠CEH=90°,
∴∠BEC=∠GEH,
∵∠CDF=180°-90°=90°,DF=DC,
∴∠DCF=45°,
∴∠CHE=45°,∠BCE=135°,
∴CE=HE,∠GHE=135°,
∴∠BCE=∠GHE,
在△BCE和△GHE中,
$\left\{\begin{array}{l}{∠BEC=∠GEH}&{\;}\\{CE=HE}&{\;}\\{∠BCE=∠GHE}&{\;}\end{array}\right.$,
∴△BCE≌△GHE(ASA),
∴BE=GE,
∴BN⊥NE;
(3)解:设CE=a,则EF=2a,CF=3a,
∴CD=BC=AB=AD=$\frac{3\sqrt{2}}{2}$a,CH=$\sqrt{2}$a,
∴DH=$\frac{\sqrt{2}}{2}$a,
∵△BCE≌△GHE,
∴GH=BC=$\frac{3\sqrt{2}}{2}$a,
∴DG=$\sqrt{2}$a,
∴BM=$\sqrt{2}$a,
∴AM=$\frac{\sqrt{2}}{2}$a,
∴tan∠ADM=$\frac{AM}{AD}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{3\sqrt{2}}{2}}$=$\frac{1}{3}$.
点评 本题是四边形综合题,考查了正方形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,等腰直角三角形的判定与性质,锐角三角函数等知识;难度较大,综合性强,通过作辅助线构造出全等三角形与等腰直角三角形是解题的关键,也是解题的难点.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )| A. | -3 | B. | -2 | C. | -2.5 | D. | -3.5 |
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高 如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?
如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?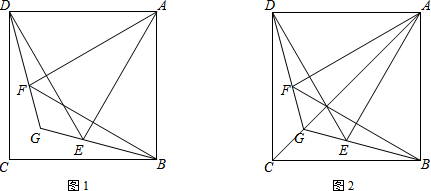
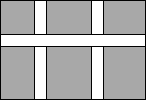 如图,要在长100米,宽90米的矩形绿地上,修建三条宽度相同的道路,剩下6块绿地面积共8448平方米,求道路宽.
如图,要在长100米,宽90米的矩形绿地上,修建三条宽度相同的道路,剩下6块绿地面积共8448平方米,求道路宽.