题目内容
13.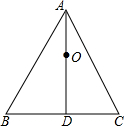 如图,△ABC是边长为2$\sqrt{3}$的等边三角形,AD⊥BC于点D,以AD的中点O为圆心作一个半径为0.75的⊙O,问:⊙O与△ABC的各边有何位置关系?请说明理由.
如图,△ABC是边长为2$\sqrt{3}$的等边三角形,AD⊥BC于点D,以AD的中点O为圆心作一个半径为0.75的⊙O,问:⊙O与△ABC的各边有何位置关系?请说明理由.
分析 作OE⊥AB于E,作OF⊥AC于F,由等边三角形的性质得出BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$,∠BAD=$\frac{1}{2}$∠BAC=30°,得出AD=$\sqrt{3}$BD=3,求出OA,由含30°角的直角三角形的性质得出OE=OF=0.75,得出⊙O与AB、AC相切,由OD>0.75,得出⊙O与BC相离.
解答 解:⊙O与AB、AC相切,⊙O与BC相离;理由如下:
作OE⊥AB于E,作OF⊥AC于F,如图所示:
∵△ABC是等边三角形,AB=BC=AC=2$\sqrt{3}$,∠BAC=60°,
∵AD⊥BC,
∴AD平分∠BAC,BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴AD=$\sqrt{3}$BD=3,
∵O为AD的中点,
∴OA═OD=$\frac{1}{2}$AD=1.5,
∴OE=OF=$\frac{1}{2}$OA=0.75,
∵OE⊥AB,OF⊥AC,
∴⊙O与AB、AC相切;
∵OD>0.75,
∴⊙O与BC相离.
点评 本题考查了直线与圆的位置关系的判定方法、等边三角形的性质、含30°角的直角三角形的性质、角平分线的性质定理;本题综合性强,熟练掌握直线与圆的位置关系的判定方法是解决问题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
18.个人取得薪金、工资所得应缴纳个人所得税.2008年3月1日起个人所得税的起征点由1600元提高到2000元.工资扣除2000元部分为全月应纳税所得额.全月应纳税所得额税率见下表:
(1)小明的爸爸2008年5月份的工资是1800元,6月份的工资是2400元,7月份的工资是2600元.按照个人所得税法规定,小明的爸爸这三个月各应缴纳个人所得税多少元?
(2)小强的爸爸2008年7月份缴纳的个人所得税是235元,他这个月实际领的工资多少元?
(3)小亮的爸爸某月纳税265元,他这个月工资是多少元,实际领到工资多少元?
| 全月应缴税所得额 | 税率/% |
| 不超过500元的 | 5 |
| 超过500元至2000元的部分 | 10 |
| 超过2000元至5000元的部分 | 15 |
| 超过5000元至20000元的部分 | 20 |
(2)小强的爸爸2008年7月份缴纳的个人所得税是235元,他这个月实际领的工资多少元?
(3)小亮的爸爸某月纳税265元,他这个月工资是多少元,实际领到工资多少元?
5.观察下列图形:按照这样的规律,第n个图形有( )个★.


| A. | 3n-1 | B. | 3n+1 | C. | 3n+4 | D. | 4n+3 |
2.一根铁丝长32厘米,将它围成一个长和宽都是整厘米数的长方形,有多少种不同的围法?列表解决,并算出它们的面积.
比较它们的长、宽和面积,你有什么发现?
| 长/厘米 | ||
| 宽/厘米 | ||
| 面积/平方厘米 |
 △ABC中,∠A=50°,∠B=70°,以AB为直径的⊙O交AC、BC于E、F两点,判断△OEF形状,并说明理由.
△ABC中,∠A=50°,∠B=70°,以AB为直径的⊙O交AC、BC于E、F两点,判断△OEF形状,并说明理由.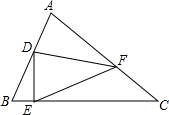 如图,在△ABC中,∠ACB=45°,D是AB边的中点,点E在BC边上,点F在AC边上,DE⊥DF,连接EF,若BE=1,EF=5,则线段AF的长为3$\sqrt{2}$.
如图,在△ABC中,∠ACB=45°,D是AB边的中点,点E在BC边上,点F在AC边上,DE⊥DF,连接EF,若BE=1,EF=5,则线段AF的长为3$\sqrt{2}$.