题目内容
3. △ABC中,∠A=50°,∠B=70°,以AB为直径的⊙O交AC、BC于E、F两点,判断△OEF形状,并说明理由.
△ABC中,∠A=50°,∠B=70°,以AB为直径的⊙O交AC、BC于E、F两点,判断△OEF形状,并说明理由.
分析 根据等腰三角形的性质得到∠AEO=∠A=50°∠OFB=∠B=70°,根据圆内接四边形的性质得到∠CEF=∠B=70°,∠CFE=∠A=50°,由平角的定义得到∠OEF=∠EFO=180°-70°-50°=60°,即可得到结论.
解答 解:△OEF是等边三角形,
理由:∵OA=OE,OF=OB,
∴∠AEO=∠A=50°∠OFB=∠B=70°,
∵∠CEF=∠B=70°,∠CFE=∠A=50°,
∴∠OEF=∠EFO=180°-70°-50°=60°,
∴△OEF是等边三角形.
点评 本题考查了圆周角定理,圆内接四边形的性质,等边三角形的判定,平角的定义,熟记各定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.若方程x-(2a+1)=3x+(3a+2)的解是x=0,则a等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
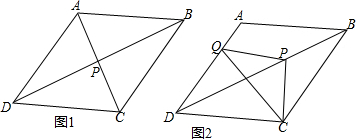
 如图,已知A,B,C,D四点共圆,且AC=BC.求证:DC平分∠BDE.
如图,已知A,B,C,D四点共圆,且AC=BC.求证:DC平分∠BDE. 如图,D是△ABC中BC边上任意一点,求证:2AD<AB+BC+AC.
如图,D是△ABC中BC边上任意一点,求证:2AD<AB+BC+AC.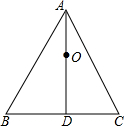 如图,△ABC是边长为2$\sqrt{3}$的等边三角形,AD⊥BC于点D,以AD的中点O为圆心作一个半径为0.75的⊙O,问:⊙O与△ABC的各边有何位置关系?请说明理由.
如图,△ABC是边长为2$\sqrt{3}$的等边三角形,AD⊥BC于点D,以AD的中点O为圆心作一个半径为0.75的⊙O,问:⊙O与△ABC的各边有何位置关系?请说明理由.