题目内容
20.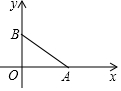 如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
分析 如图,作B1C⊥x轴于C,先利用勾股定理就是出OB=3,再利用旋转的性质得BA=A B1,且∠BA B1=90°,
接着证明△ABO≌△B1AC得到AC=OB=3,B1C=OA=4,然后写出B1点的坐标.
解答 解:如图,作B1C⊥x轴于C,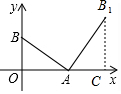
∵OA=4,AB=5,
∴OB=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵线段BA绕点A沿逆时针旋转90°得A B1,
∴BA=A B1,且∠BA B1=90°,
∴∠BAO+∠B1AC=90°
而∠BAO+∠ABO=90°,
∴∠ABO=∠B1AC,
在△ABO和△B1AC中
$\left\{\begin{array}{l}{∠AOB=∠{B}_{1}CA}\\{∠ABO=∠{B}_{1}AC}\\{AB={B}_{1}A}\end{array}\right.$,
∴△ABO≌△B1AC,
∴AC=OB=3,B1C=OA=4,
∴OC=OA+AC=7,
∴B1点的坐标为(7,4).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
15.下列各对近似数中,精确度一样的是( )
| A. | 0.28与0.280 | B. | 0.70与0.07 | C. | 5百万与500万 | D. | 1100与1.1×103 |
12.已知二次函数y=x2-4x-5,若y>0,则( )
| A. | x>5 | B. | -1<x<5 | C. | x>5或x<-1 | D. | x>1或x<-5 |
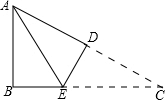 如图所示,在△ABC中,AB=5,BC=7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为12.
如图所示,在△ABC中,AB=5,BC=7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为12.