题目内容
10.商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台.为了促销,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4800元,同时又要使消费者得到更多实惠,每台冰箱应降价( )| A. | 100元 | B. | 200元 | C. | 300元 | D. | 400元 |
分析 利用每一台冰箱的利润×每天售出的台数=每天盈利,设出每台冰箱应降价x元,列方程解答即可.
解答 解:设每台冰箱应降价x元,每件冰箱的利润是:(2400-2000-x)元,卖(8+$\frac{x}{50}$×4)件,
列方程得,
(2400-2000-x)(8+$\frac{x}{50}$×4)=4800,
x2-300x+20000=0,
解得x1=200,x2=100;
要使百姓得到实惠,只能取x=200,
故选B.
点评 此题考查了一元二次方程的应用,基本数量关系:每一台冰箱的利润×每天售出的台数=每天盈利.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.填在如图各正方形中的四个数之间都有一定的规律,按此规律得出a、b的值分别为( )
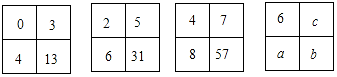

| A. | 10、91 | B. | 12、91 | C. | 10、95 | D. | 12、95 |
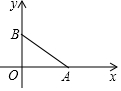 如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
 作图题:尺规作图(不写过程,保留作图痕迹).
作图题:尺规作图(不写过程,保留作图痕迹).