题目内容
5.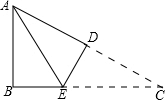 如图所示,在△ABC中,AB=5,BC=7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为12.
如图所示,在△ABC中,AB=5,BC=7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为12.
分析 首先根据翻折变换的性质,可得AE=CE,然后根据三角形的周长的求法,可得△ABE的周长等于AB和BC的长度和,据此解答即..
解答 解:∵将△ABC折叠,使点C与点A重合,折痕为DE,
∴AE=CE,
∴△ABE的周长=AB+BE+AE
=AB+(BE+CE)
=AB+BC
=5+7
=12(cm),
即△ABE的周长为12cm.
故答案为:12cm
点评 此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
10.下列四个实数中,最大的是( )
| A. | -2 | B. | 0 | C. | -$\sqrt{2}$ | D. | $\sqrt{3}$ |
14.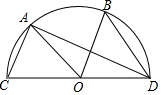 如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
 如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )
如图,CD是⊙O的直径,A,B两点在圆上,且AC∥OB,∠ADB=33°,则∠ADC的度数等于( )| A. | 24° | B. | 28° | C. | 30° | D. | 33° |
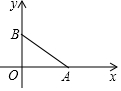 如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标. 小敏在作⊙O的内接正五边形时.先做了如下几个步骤:
小敏在作⊙O的内接正五边形时.先做了如下几个步骤: